Example   Solve each of the following systems of equations.

             5x + 4 y = 1

             3x - 6 y = 2

Solution

It is the system in the previous examples which made us work with fractions.  Working it here will illustrate the differences among the two methods and it will also illustrate that either method can be utilized to get the solution to a system.

Thus, we have to multiply one or both equations through constants so that one of the variables has the similar coefficient with opposite signs.  Thus, since the y terms already have opposite signs let's worked along these terms.  It looks like if we multiply the first equation by three and the second equation by two the y terms will have coefficients of 12 and -12 that is what we require for this method.

Following is the work for this step.

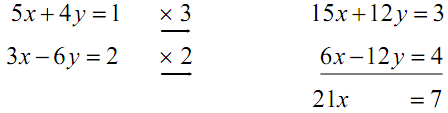
Thus, as the description of the method promised we have an equation which can be solved for x.

Doing this gives, x = 1/3 that is exactly what we found in the previous example.  However Notice that the only fraction which we had to deal along with to this point is the answer itself that is different from the method of substitution.

Now, again don't forget to determine y.  In this case it will be a bit more work than the method of substitution. To determine y we have to substitute the value of x in either of the original equations & solve for y.  As x is a fraction let's notice that, in this case, if we plug this value in the second equation at least temporarily we will lose the fractions.  Note that frequently this won't happen and we'll be forced to deal along with fractions whether we want to or not.

3 ( 1 /3) - 6 y = 2

1 - 6 y = 2

-6 y = 1

y = - 1/6

Again, it is the similar value we found in the previous example.