Solve x =√(x+ 6) .

Solution

In this equation the fundamental problem is the square root.  If it weren't there we could do the problem.  The whole procedure that we're going to go through here is set up to remove the square root. Though, as we will see, the steps which we're going to take can in fact cause problems for us.  Thus, let's see how this all works.

Let's notice that if we just square both of sides we can make the square root go away.  Let's do that & see what happens.

( x)²  = ( √(x + 6) )²

x²  = x +6

x² - x - 6 =0

( x - 3) ( x + 2) =0       ⇒x = 3,      x = -2

Upon squaring both of sides we see that we get a factorable quadratic equation which gives us two solutions x = 3 and x = -2 .

Now, for no clear reason, let's do something which actually we haven't done since the section on solving linear equations. Let's check our answers. Recall as well that we have to check the answers in the original equation! That is very significant.

Let's first check    x = 3

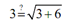
      3 = √9        OK

Thus x = 3 is a solution.  Now let's check x = -2 .

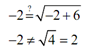                                                         NOT OK

We have a problem.  Remember that square roots are always +ve and thus x = -2 does not work in original equation.  Here one possibility is that we commit a mistake somewhere. We can go back & look though and we'll rapidly see that we haven't made a mistake.

Thus, what is the deal?  Recall that our first step in the solution procedure was to square both sides.  Notice that if we plug x = -2 into the quadratic we solved out it would actually be a solution to that.  While we squared both sides of the equation actually we changed the equation and in the procedure introduced a solution that is not a solution to the original equation.

With these problems this is critically important that you check your solutions as it will often happen. While this does we only take the values which are actual solutions to the original equation.

Thus, the original equation had a single solution x = 3.