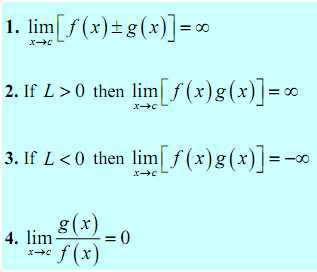Evaluate following limits.

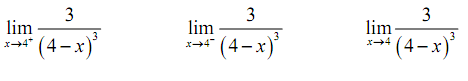
Solution

Let's begin with the right-hand limit.  For this limit we have,

x > 4  ⇒          4 - x < 0          ⇒ ( 4 - x )³  = 0      also, 4 - x → 0  as x → 4 .  Therefore, we contain a positive constant divided by an increasingly small -ve number. The results will be an increasingly large -ve number and hence it looks like the right-hand limit will be negative infinity.

For the left-handed limit we have following,

x < 4 ⇒           4 - x > 0          ⇒ ( 4 - x )³  > 0 and still we have, 4 - x → 0  as x → 4 .  In this case we contain a positive constant divided by an increasingly small +ve number.  The results will be an increasingly large positive number and hence it looks like the left-hand limit will be positive infinity.

The normal limit will not present since the two one-sided limits are not the similar.  The official answers to this example are then,

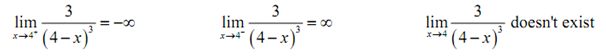
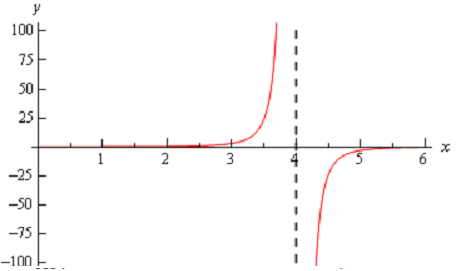
Following is a quick sketch to verify our limits.

Facts

Given the functions f ( x )& g ( x ) assume we have,

for some real numbers c & L. Then,