Example of Trig Substitutions

Evaluate the subsequent integral.

∫ √((25x² - 4) / x) (dx)

Solution

In this type of case the substitution u = 25x² - 4 will not work and so we are going to must do something dissimilar for this integral.

It would be great if we could get rid of the square root someway. The following substitution will do that for us.

X = 2/5 sec θ

Do not be anxious about where this came from at this point. As we work with this problem you will see that it works and that if we have a identical type of square root in the problem we can all time make use of a similar substitution. Previous to we actually do the substitution though let's confirm the claim that this will permit us to get rid of the square root.

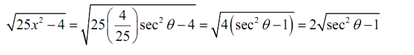
To get relieve of the square root all we require to do is recall the relationship,

tan² θ + 1 = sec² θ  ⇒ sec² θ -1 = tan² θ

By using this detail the square root becomes,

√(25x² - 4) = 2 √tan² θ = 2|tan θ |

Note the existence of the absolute value bars there. These are significant.  Recall that

√x² = |x|

There should all time be absolute value bars at this stage.  If we knew that tan θ was all time positive or all time negative we could remove the absolute value bars using,

|x| = x= if x > 0 or -x if x<0

With no limits we won't be capable to ascertain if tan θ is positive or negative, though, we will requires to eliminate them in order to do the integral. Hence, as we are doing an indefinite integral we will presume that tan θ will be positive and thus we can drop the absolute value bars. This illustrates,

√(25x² - 4) = 2 tan θ

Thus, we were able to remove the square root by using this substitution.  Let's now do the substitution and see what we obtain.  In doing the substitution remember that we'll as well need to substitute for the dx. This is easy enough to get from the substitution.

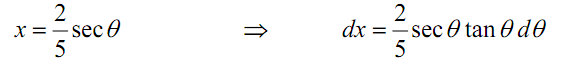
x = 2/5 sec θ ⇒ dx = 2/5 sec θ tan θ d θ

By using this substitution the integral becomes,

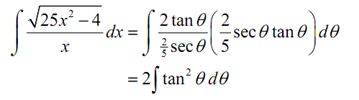
With this kind of substitution we were capable to eliminate the given integral to an integral involving trig functions and we saw how to do these problems in the preceding section.  Let's end the integral.

∫ √ (25x² - 4)/x (dx) = 2∫ sec² θ - 1d θ

=2(tan θ - θ) + c

Thus, we've got an answer for the integral.  Regrettably the answer isn't given in x's as it should be.  Thus, we require to write our answer in terms of x. We can do this along with some right triangle trig. From our original substitution we comprise,

sec θ = 5x/2 = hypotenuse / adjacent

This provides the following right triangle.

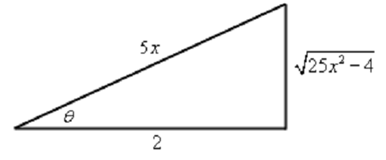
From this we can see that,

tan θ = √((25x² - 4) / 2)

We can deal along with the θ in one of any range of ways.  From our substitution we can see that,

θ = sec^-1 (5x/2)

While this is a completely acceptable technique of dealing with the we can make use of any of the possible six inverse trig functions and as sine and cosine are the two trig functions most people are known with we will generally use the inverse sine or inverse cosine. In this case we will use the inverse cosine.

θ = cos^-1 (2/5x)

Thus, with all of this the integral becomes

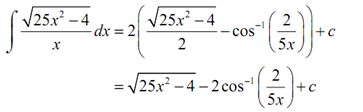
We now have the solution back in terms of x.