Evaluate the deflection at the free end of the cantilever:

Discover the slope and deflection at the free end of the cantilever illustrated in Figure . Take EI = 200 × 10⁶ N-m².

Solution

Apply Udl in both the upward and downward directions in the portion CB.

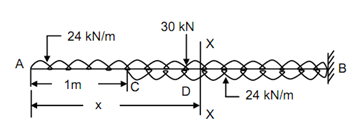
 Figure

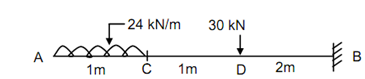
 Figure

M = - 24 x . (x/2) + 24 ( x - 1) (( x - 1)/2) - 30 [ x - 2]

= - 12 x²  + 12 [ x - 1]²  - 30 [ x - 2] --------- (1)

EI (d ² y /dx² )= M = - 12 x 2  + 12 [ x - 1]² - 30 [ x - 2]        ----------- (2)

EI dy/ dx = - 4 x³ + 4 [ x - 1]³ - 15 [ x - 2] ²+ C₁        --------- (3)

EIy =- x + [ x - 1] - 5 [ x - 2] + C₁ x + C₂            --------------- (4)

The boundary conditions are :

 At B, x = 4 m, dy/ dx  = 0         -------- (5)

At B, x = 4 m,  y = 0                       ----------- (6)

From Eqs. (3) and (5)

0 = - 4 × 4 ³+ 4 (4 - 1) ³- 15 (4 - 2)₃ + C₁

∴          C₁ = 208                   ----------- (7)

 From Eqs. (4), (6) and (7)

0 =- 4 ⁴+ (4 - 1)⁴ - 5 (4 - 2) ³+ 208 × 4 + C₂

∴          C₂  = - 617                  --------- (8)

∴          EI (dy / dx )=- 4 x³  + 4 [ x - 1]³  - 15 [ x - 2]²  + 208         ---------- (9)

EIy =- x⁴  + [ x - 1]⁴  - 5 [ x - 2]³  + 208 x - 617-------- (10)

At free end A, x = 0, From Eq. (9)

 θ _A = + 208 /EI = + 208 × 10/200 × 106 = + 1.04 × 10^{- 3}  radians

From Eq. (10)

y_A  =     617/EI = - 617 × 10³ × 10³ / 200 × 10⁶ = - 3.085 mm ( ↓ )