Evaluate the acceleration of the three weights:

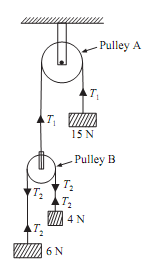
A system of weight connected by the string passing over pulleys A and B is shown in figure given below. Find out acceleration of the three weights. Assume the weightless string and ideal condition for the pulleys.

Sol: As strings are weightless and ideal conditions prevail, thus the tensions in string passing over pulley A will be same. The tensions in string passing over pulley B will be same. But tensions in the strings passing over pulley A and over pulley B will be different as shown in the given figure.

Let T₁  = Tension in string passing over pulley A
T₂  = Tension in string passing over pulley B

One end of string passing over pulley A is connected to the weight 15N, and other end is connected to pulley B. As weight 15N is more than weights (6 + 4 = 10N), thus weight 15N will move downwards, while pulley B will move upwards. The acceleration of weight 15N and of pulley B will be same.

Let, a  = Acceleration of block 15N in the downward direction1  = Acceleration of 6N downward with respect to the pulley B.

Then acceleration of weight 4N with respect to the pulley B = a₁  in upward direction.

The absolute acceleration of weight 4N,

= Acceleration of 4N with respect pulley B + Acceleration of pulley B. = a₁ + a (upward)

(as both the acceleration are in upward direction, total acceleration will be the sum of the two accelerations)

Absolute acceleration of weight 6N,

= Acceleration of 6 with respect to pulley B + Acceleration of pulley B.

= a₁ - a (downward)

(As a₁ is acting downward while a is acting upward. Thus total acceleration in downward direction)

Consider motion of weight 15N Net downward force = 15 - T₁

Using F = ma,

15 - T₁ = (15/9.81)a                                                                                                                         ...(1)

Consider motion of weight 4N

Net downward force = T₂  - 4

Using F = ma,

T₂  - 4 = (4/9.81)(a + a₁)                                                                                                               ...(2)

Consider the motion of weight 6N

Net downward force = 6 - T₂

Using F = ma,

6 - T₂ = (6/9.81)(a₁ - a)                                                                                                                ...(3)

Consider motion of pulley B,

T₁=2T2                                                                                                                                         ...(4)

Adding equation (2) and (3)

2 = (4/9.81)(a + a₁) + (6/9.81)(a₁ - a)

9.81 = 5a₁ - a                                                                                                                               ...(5)

Multiply equation (2) by 2 and put value of equation (4),

T₁  - 8 = (8/9.81)(a₁  + a)                                                                                                                ...(6)

Add equation (1) and (6), we get

15 - 8 = (15/9.81)a + (8/9.81)(a₁  + a)

23a + 8a₁ = 7 X 9.81                                                                                                                           ...(7)

Multiply equation (5) by 23 and add with equation (7),

a₁ = 2.39m/sec²                                                                                                                         .....ANS

Putting value of a₁ in equation (5),

a = 2.15m/sec²                                                                                                                            ....ANS

Acceleration of weight 15N = a = 2.15m/sec²                                                                   ......ANS

Acceleration of weight 6N = a = 0.24m/sec²                                                                     .......ANS

Accelerationofweight  4N = a = 4.54m/sec²                                                                      .......ANS