The statement of Gustafson's law can be described with the help of an illustration. Let us take a problem, say P, which has to be solved using a parallel computer. Let Ts be the time taken which is in use as constant for implementing sequential operations. Let Tp (N, L) be the time taken for running the parallel operations with L as total load on a parallel computer with N processors. The total time taken for finding the answer of problem is T=Ts + Tp. Thus, S (N) can be calculated as under:

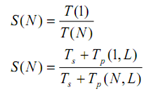
Also, Tp (1, L)= N* Tp (N, L) i.e. time taken to implement parallel operations having a load of L on one processor is equivalent to the N multiplied by the time taken by one computer having N processor. If α be the fraction of sequential load for a given problem i.e.

α =          Ts / Ts + T p ( N , L)

Substituting Tp (1, L)= N* Tp (N, L) we find,

S (n) =   Ts + N * T p ( N , L) / Ts +T p( N , L)

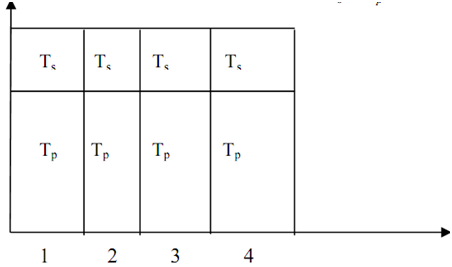
Fixed Execution Time for Gustafson's Law

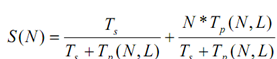
Now, let us change the total equation of S(N) in the form of X. We get

S(N) = α +N * (1-α)

S (N) = N -α * (N-1)

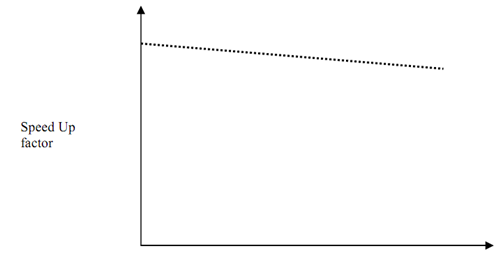
Now, let us put some values of α and compute the speed up factor for increasing values of α i.e. sequential factor of work load for a fixed number of processors say N.  Figure shows a pictorial view of effect of Gustafson's Law on the speed up factor. The graph illustrate as the value of α increases, the speed up factor increases. This decrease is because of overhead caused by inter-processor communication.

α  (Sequential Operations)

Figure: S (N) vs. α (Graph is not to scale)