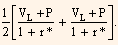The value of node is determined using a methodology called backward induction. The value at any node depends on the future cash flows; therefore, we need to start from the last year in the tree and work backwards to get the required solution. For example, if we want to find the value at node T, we need to first calculate the value at node T_H and T_L and to find the value of bond at node T_H; also, we need to first calculate the value of the bond at nodes T_HH and T_HL which is nothing but the future cash flows. The future cash flows depend on two factors. First, the coupon payment one year from now; and second, the bonds value one year from now. We have already seen that at every node there are two options and the node can take a higher or lower value. Therefore, the cash flow at a node can either be the bond value if the 1-year rate is higher rate plus the coupon payment or the bond value if the 1-year rate is lower rate plus the coupon payments. Coming back to our example, the cash flow at T will either be bond rate at T_HH plus coupon rate or the bond rate at T_HL plus coupon payment.

We need to calculate the present value of the expected cash flow to get the bond value at a node. We get two present values in each case, one is the present value if the 1-year rate is higher and the other if it is lower. As we have two options with equal probability, an average of the two present values is computed.

V_H     =       Higher 1-year rate value of the bond.

V_L       =       Lower 1-year rate of the bond.

P       =       Coupon payment.

r*      =       1-year rate at the node where the valuation is sought.

Therefore, the cash flow at a node is

V_H + P for the higher 1-year rate (or)

V_L+ P for the lower 1-year rate.

Present value of the cash flows using the 1-year rate at the node, is calculated as follows:

Present value for the higher rate =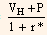 

Present value for the lower rate =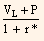 

The value of the bond at the node is