Find the solution to the subsequent IVP.

ty' - 2y = t⁵ sin(2t) - t³ + 4t⁴, y (π) = 3/2 π⁴

Solution: First, divide by t to find the differential equation in the accurate form.

y' - 2y/t = t⁴ sin(2t) - t² + 4t³, y (π) = 3/2 π⁴

Here remember that we have done this we can get the integrating factor, µ(t).

µ(t)  = e^{∫(- 2y/t)dt}  = e^-2In|t|

Always remember that the "-" is part of p(t).  Forgetting such minus sign can take a difficulty that is extremely easy to do and turn it in an extremely difficult, if possible trouble so be careful!

Here, we just require simplifying this as we did in the previous illustration.

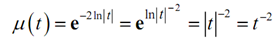
Yet again, we can drop the absolute value bars as we are squaring the term.

Here multiply the differential equation through the integrating factor as again, ensures it's the rewritten one and not the original differential equation.

(t^-2 y)' = t² sin(2t) - 1 + 4t