Determine the self inductance of the two coils:

Two coils with a coefficient of coupling of 0.6 between them are connected in series so as to magnetize (i) in the same direction, and (ii) in the opposite direction. The corresponding values of equivalent inductance are achieved as 1.8 H for (i) and 0.8 H for (ii). Determine the self inductance of the two coils and the mutual inductance between them.

Solution

Coefficient of coupling k = 0.6

(a)             For magnetization in the same direction,

 Equivalent inductance L = L₁+ L₂ + 2M

or,        1.8 = L₁+L₂ + 2M        

(b)             For magnetization in the opposite direction,

 Equivalent inductance L = L₁ + L₂ - 2M

or,        0.8 = L₁ + L₂ - 2M        

Subtracting Eq. (43) from Eq. (42), we get

                4M = 1

or,        M = 0.25 H

Adding Eq. (42) and Eq. (43), we obtain

2 (L₁ + L₂) = 2.6

or,        L₁ + L₂ = 1.3     . . . (2.44)

We know,

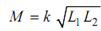
∴          L₁ L₂  =M² / k² = (0.25)² / (0.6)² = 0.1736                     

Now  (L₁ - L₂)² = (L₁ + L₂)² - 4 L₁ L₂ = (1.3) ² - 4 × 0.1736 = 0.9956

∴          L₁  - L₂  = 0.9978              

Adding Eq. (44) and Eq. (46), we obtain

∴ L₁ = 1.1489 H

L₂  = 1.3 - L₁  = 1.3 - 1.1489 = 0.1511 H