Determine the maximum stress intensities:

A rolled steel I-section, flanges 150 mm wide & 25 mm thick, web 200 mm long & 10 mm thick  is utilized to carry & axial load of 800 kN. The load line is eccentric, 50 mm above XX & 30 mm to the left of yy. Determine the maximum & minimum stress intensities in the section.

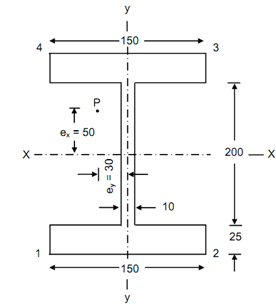
Figure

Solution

Area of the cross-section, A = 2 × (150 × 25) + (200 × 10) = 9500 mm²

Moment of inertia about XX-axis,

 I xx     = 150 × 250/12 - 140 (20)³/12

= 8565 × 10⁴  mm⁴

Moment of inertia about YY-axis,

I yy =2 × (25 × 150³ )/ 12       -200 (10)³/12 = 1407 × 10⁴  mm⁴

Eccentricity,

ex  = 50 mm

ey  =- 30 mm

Vertical load, W = 800 kN

Direct stress at any point, f₀  = P/A    =800 × 103/9500

            = 84.2 N/mm²

Maximum bending compressive stress shall take place at edge 4 of the section in Figure

 = ( fb )₄  = ((P × ex /I_xx) × y )+(( P × ey/ I _yy )× x)

= (800 × 103 × 50/ 8565 × 10⁴) × (- 125) +( 800 × 10³ × (- 30) /1407 × 10⁴) × 75

= 186.4 N/mm2

Maximum bending tensile stress shall take place at edge 2 at the section.

 ( f _b )2  =( 800 × 10 ³ × 50)/( 800 × 10⁴ ))× (- 125)

                    +( 8565 × 10³ (- 30)/ (1407 × 10⁴ ))× 75

              = - 18.64 N/mm²

In the section Resultant stress would be as follows:

Maximum at corner 4 = 84.2 + 186.4 = 270.6 N/mm²

Minimum at corner 5 = 84.2 - 186.4 = - 102.2 N/mm²          (tensile)