Determine the maximum bending stresses:

A rectangular beam of breadth 100 mm & depth 200 mm is simply supported over a span of 4 m. The beam is loaded with a uniformly distributed load of 5 kN/m over the whole span. Determine the maximum bending stresses.

Solution

Breadth of beam, b = 100 mm

Depth of beam, d = 200 mm

Moment of inertia, I =1 /12 bd³ = ( 1/12 )× 100 × (200)³ = 66.67 × 106 mm4

Span of beam, I = 4 m

Uniformly distributed load, w = 5 kN/m

Maximum bending moment at centre of beam,

M = wl ²/8  =5 × 4 ²/8

= 10 kN m = 10⁷ N mm

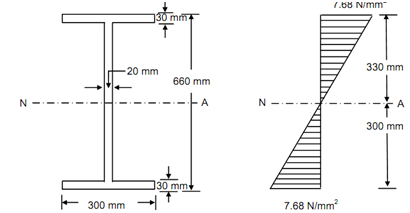
(1)   Cross-section of Beam                    (2) Bending Stress Distribution

Figure

Neutral axis passes by the centre of section.

The distance of top and bottom layer from neutral axis, y = 100 mm

Thus, Bending stress, σ = (M/ I) × y

= (10⁷ )/(66.67 × 10⁶) × 100

= 15 N/mm²

Thus the extreme bending stresses are 15 N/mm². Figure illustrated the bending stress distribution for this rectangular section.