Determine reactions of the overhanging beam:

Determine reactions at points A and B of the overhanging beam as shown in the figure given below.

First change UDL in point load.

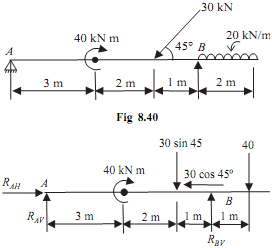
Figure

Resolve all the forces in horizontal direction and vertical direction. As hinged at point A (one vertical and horizontal reaction).

Let reaction at hinged that is, point A is R_AH and R_AV, Let ∑H & ∑V is the sum of horizontal and vertical component of forces, The supported beam is in equilibrium, thus Draw the free body digram of the beam as shown in the given figure, As beam is in equilibrium, that is

R_AH = 30 cos45° = 21.2KN

R_AH = 21.21KN                                                               .......ANS

∑V = 0;

R_AV  -30 sin45 - 40 + R_BV  = 0

R_AV + R_BV = 61.2KN                                                                                                                          ...(i)

By taking moment about B,

R_AV  × 6 + 40 - 30 sin45 × 1 + 40 × 1 = 0

R_AV = - 9.8 KN              .......ANS

Putting value of R_AV in the equation (i), we get

R_BV = 71KN          .......ANS

Thus reaction at support A that is R_AV  = -9.8KN, R_AH  = 21.2KN, R_BV  = 71KN