Determine moment of this normal force - rectangular beam:

A rectangular beam contains a width of 100 mm and a depth of 200 mm. This is utilized as a simply supported beam & the maximum bending stress is restricted to 10 N/mm2. Then determine the following :

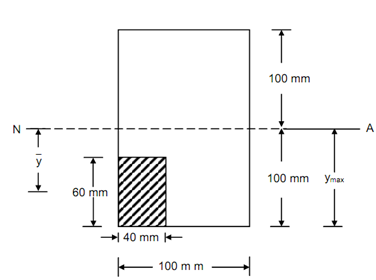
 (a) Entire normal force on the left bottom corner area of size 40 mm × 60 mm, and

(b) moment of this normal force around the neutral axis.

Solution

Maximum bending stress, σ_max = 10 N/mm²

Normal force on the shaded area, left bottom corner  is following

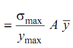
=   (10/100) × (40 × 60) × (40 + 30)

Here, A = Shaded area = 40 × 60 mm²

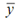=   Centroid of shaded area through the neutral axis

= (100 - 60) + ( 60/2) = (40 + 30) = 70 mm

Figure

∴ Normal force on the partial beam section is following

 =   (10/100) × 2400 × 70 = 16800 N = 16.8 N

The partial area is subjected into a tensile force

∴ Normal force on partial beam section = 16.8 kN (tension)

Moment of the force around the neutral axis

= (σ_max / y_max) × I_s

I_s = Moment of inertial of the shaded area around the neutral axis

=   (1/12)  × 40 × (60)³  + (40 × 60) × (70)²  = 1248 × 10⁴  mm⁴

∴ Moment of normal force around the neutral axis

=  ( 10 /100) × 1248 × 10⁴  = 1248 × 10³  Nm = 1248 m