Determine modulus of resilience:

A steel specimen of 10 mm diameter & 50 mm gauge length was tested in tension and following observations were recorded.

Load at upper yield point = 20600 N

 Load at lower yield point = 19650 N

Maximum load = 35550 N

Gauge length after fracture = 62.43 N

Determine modulus of resilience and modulus of toughness. Also compute % elongation. E = 210 × 10³  N/mm² .

Solution

Area of cross-section of specimen,

A₀  = (π/4 ) d ²

A ₀ = (π /4 )(10) ²  = 78.57 mm2

∴          Yield strength,

σ _Y = 19650 /78.57 = 250 N/mm²

Ultimate tensile strength, σ _u  = 35550 /78.57 = 452.5 N/mm²

            Strain at fracture or % elongation =ε _f = 62.43 - 50 = 0.25 or 25%

∴          Modulus of resilience  =

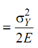
=          (250)²  /2 × 210 × 10³ N-mm/mm³

= 148.8 × 10^{- 3}  N-mm/mm³

(i)                  (Compare with Example 1 to note that for higher yield strength modulus of resilience is larger).

Modulus of toughness =       (s_u  +s_Y /2)   ε _f

                                      = (452.5 + 250 /2 )× 0.25 N-mm/mm3

                                     = 87.8 N-mm/mm³

% elongation = 25%