Determine Maximum fibre stress:

A beam of rectangular section of 80 mm to 120 mm carries a uniformly distributed load of 40 kN/m over a span of 2 m an axial compressive force of 10 kN. Determine

1.      Maximum fibre stress,

2.      Fibre stress at a point 0.50 m from the left end of the beam & 40 mm below the neutral axis.

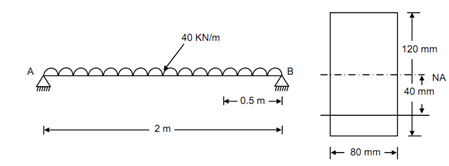
                                     (1) Loading                                          (2) Cross-section

Figure

Solution

Bending moment, M = (w × e ²) /8= (40 × 2²)/8 = 20 kN-m = 20 × 10⁶  N-mm

Section modulus, Z = (1/6) × 80 × (120)²  = 1.92 × 10⁵  mm³

Moment of inertial, I = (1/12) × (80) × (120)³ = 11.52 × 10⁶  mm⁴

Axial load, P = 10 kN = 10 × 10³  N

Direct stress, f₀  = P/A =10 × 10³/ (80 × 120) = 1.04 N/mm²

Bending stress,  f b =± M/ Z  =( 20 × 10⁶ )/(1.92 × 10⁵) = ± 104.16 N/mm2

∴          Maximum fibre stress = 1.04 + 104.16 = 105.20 N/mm² (compressive)

∴          Bending moment at 0.50 m from left end will be,

M = ( - 40 × 0.50 + 40 × 0.50² / 2)

= - 15 kN-m

= 15 × 10⁶  N-mm (sagging)

∴          Bending stress at 40 mm below the neutral axis will be,

= (M/I) . y

= (15 × 10⁶ )/(11.52 × 106 ) × (- 40)

=- 52.08 N/mm²  (tensile)

∴          Resultant fibre stress = 1.04 - 52.08

                                             =- 51.04 N/mm² (tensile)