Q. Regard as a program that reads a set of Data for 'n' no. of triangles. The program reads three integer values like representing the sides of triangles. The program prints for each triangle whether the triangle is isosceles or equilateral or a simple. Develop logic as well as do the following:

(i) Compute cyclomatic complexity?

(ii) Design test cases for loop testing?

Ans.                 The program logic will be like follows:

Enter three sides of a triangle.

Read a, b and c

If(a

Then is_a_triangle=TRUE

Else is_a_triangle=FALSE;

IF is_a_triangle

Then

If(a=b)XOR(a=c)XOR(b=c) AND NOT ((a=b)AND(a=c))

Then print "Triangle is Isosceles"

If(a=b)AND(b=c)

Then print "Triangle is Equilateral"

If(a<>b)AND (a<>c) AND(b<>c)

Then print "Triangle is scalene"

Else

Print "Not a triangle"

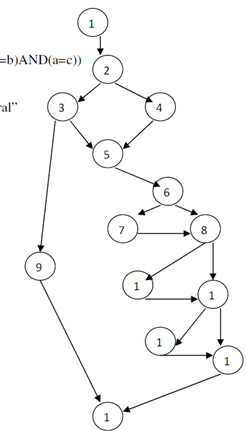
The flow graph of the problem is given as in

the fig:

(i) There are 6 independent paths i.e.

1,2,3,9,14

1,2,4,5,6,8,11,13,14

1,2,3,5,6,8,11,13,14

1,2,4,5,6,7,8,11,13,14

1,2,4,5,6,8,10,11,13,14

1,2,4,5,6,8,11,12,13,14

Cyclomatic complexity is 6

(ii) Few test cases are: