Dependent system example

Example: Solve the given system of equations.

2x + 5 y = -1

-10x - 25 y = 5

Solution

In this instance it looks like elimination would be the easiest method.

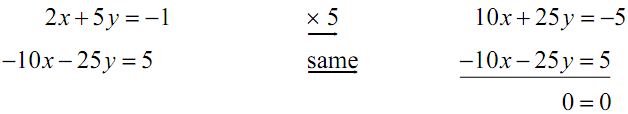
On primary glance it might appear to be the similar problem as the previous example. Though, in that case we ended up with an equality which simply wasn't true.  In this case we have 0=0 and i.e. a true equality and thus in that sense there is nothing wrong with this.

However, it is clearly not what we were expecting for an answer at this point and so we have to determine just what is going on.

We'll leave it to you to check out this, but if you determine the slope & y-intercepts for these two lines you will determine that both lines have accurately the same slope & both lines have accurately the same y- intercept.  Thus, what does it mean for us? Well if two lines have the similar slope and the same y- intercept then the graphs of the two lines are the similar graph.  In other terms, the graphs of these two lines are the same graph.  In these cases any set of points which satisfies one of the equations will also satisfy the other equation.

Also, remember again that the graph of an equation is nothing more than the set of all points which satisfies the equation.  In other terms, there is an infinite set of points which will satisfy this set of equations.

In these cases we do desire to write down something for a solution.  Thus what we'll do is solve out one of the equations for one of the variables (it doesn't matter which you select). We'll solve the first for y.

2x +5 y = -1

5 y = -2 x -1

y = - 2/5 x - 1/5

Then, given any x we can determine a y and these two numbers will make a solution to the system of equations.  Usually we denote this by writing the solution as follows,

x = t

y = -2/5 t - 1/5

where t refer for any real number

Thus show that these give solutions let's work through a couple of values of t.

t=0

x = 0                              y = - 1/5

To illustrates that it is a solution we have to plug it into both  of the equations in the system.

             -1= -1                                                     5=5

hence, x = 0 and y = - 1 /5 is a solution to the system.  Let's do another one quickly.

t=-3

x = -3                    y = - 2 /5( -3) - 1/5 = 6/5 - 1/5 = 1

Again we have to plug it into both equations in the system to illustrate that it's a solution.

             -1 = -1                                                               5 = 5

Surely

x = -3 and y = 1 is a solution.

Hence, since there are an infinite number of possible t's there have to be an infinite number of solutions to this system & they are given by,

x = t

y = -2/5 t - 1/5

Where t refer for any real number

Systems such as called dependent.

Now we've seen all three possibilities for the solution to a system of equations.  A system of equation has either no solution, exactly one solution or infinitely many solutions.