In computers, colours are created by blending different combinations of red, green and blue. These colours are normally specified as three two-digit hexadecimal numbers in html, photoshop, gimp etc. For example, Brown is specified as A62929 to indicate the proportions of red, green and blue required. For grey shades the three proportions will always be equal. Moreover FF indicates that the colour is fully saturated. Thus red is FF0000, green is 00FF00, and blue is 0000FF. This colour system is called RGB.
Other applications, such as MATLAB require the RGB colours to be specified in terms of the fraction of each colour required. In this case, the colour is specified by three numbers between 0 and 1, with 1 representing full colour saturation. For example, Brown in this system is given as (0.65, 0.16, 0.16); while red is (1, 0, 0); green is (0, 1, 0) and blue is (0, 0, 1). This representation is referred as the RGB colour fraction.
Given that different systems are used in different applications, it is important to be able to convert between the two representations. The largest number that can be represented by a two-digit hexadecimal number is 16 FF so we know that there are 255 possible shades that can be represented. Hence, to convert the hexadecimal colour representation to a colour fraction, the following has to be done:
1. Convert each hexadecimal colour number to its decimal equivalent.
2. Divide each decimal by 255.
3. Record each fraction as the colour fraction required for that colour. Converting from a colour fraction to the hexadecimal version is the reverse of the above.
To illustrate, let us consider Brown. Its shade of red is 16 A6. As a decimal this corresponds to 166. Hence, the fraction amount of red required is 166 255 0.65. Similarly for green the decimal equivalent of 16 29 is 41. Therefore, the green colour fraction is 41 255 0.16
. The blue colour fraction for Brown is also 0.16.
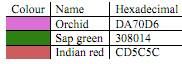
(a) Convert the RGB values for the colours below to their equivalent RGB colour fractions. Round your answers to two decimal places.