The fundamental principle is that when a tree is used to value an on-the-run issue, the resulting value should be arbitrage free i.e., it should be equal to the observed market value. Also, the interest rate tree should be consistent with the assumed interest rate volatility.

Let us, with help of an example, look at the process of constructing an interest rate tree:

The interest rate at the first node T would be the current 1-year on-the-run issue rate. The interest rate for year-one would be calculated using the coupon rate for the 2-year on-the-run issue, assumed interest rate volatility, and the interest rate at the base of the tree. Given these, the interest rates are determined on a trial and error basis. First, the lower rate r_1,L at the node T_L is assume and then using the formula (discussed earlier in this chapter) the interest rate at the higher value is calculated. It is then compared with the 2-year on-the-run issue to see if there are discrepancies in both the values; it implies that the assumption made is incorrect. If the value is too high, a higher rate guess should be made and if the value is too low a lower rate guess is to be made until the value of r_1,L is in line with the 2-year on-the-run issue.

In similar manner, rates are determined for year-two - r_2,LL, r_2,HL and r _2,HH. The information required for this task includes:

1. The coupon rate for the 3-year on-the-run issue.

2. Assumed interest rate volatility.

3. The interest rate at the base of the tree.

4. The two 1-year rates (r_1,L and r_1,H).

A guess is made of the value r_2,LL, and based on the formula discussed earlier in this chapter, the 

value of r_2,HL and r _2,HH are calculated. If the value generated by this process is not equal to the market value of the 3-year on-the-run issue, the process is to be repeated again. An iterative process is again followed. Table 2 shows the binomial interest rate tree for the issuer for valuing issues up to four years of maturity assumption volatility for the 1-year rate of 10% and Table 2 verifies that the rates on the binomial interest rate tree are the correct values. This is arrived at by showing that when the 3-year on-the-run issue is valued using backward induction method the value is 100, which is nothing but the market value of the 3-year on-the-run issue.

Table 2: Binomial Interest Rate Tree

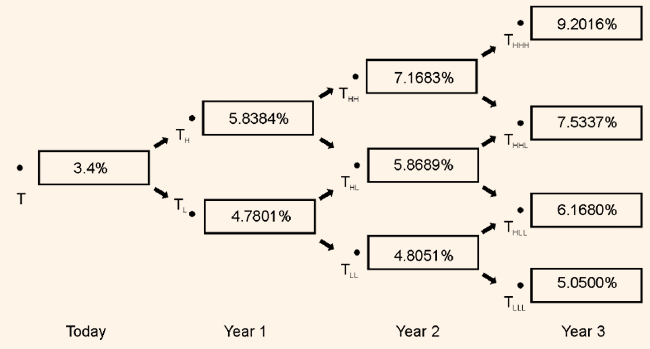
Assumed Volatility = 10%

Table 2: Verification of the Rates on the Binomial Interest Rate Tree

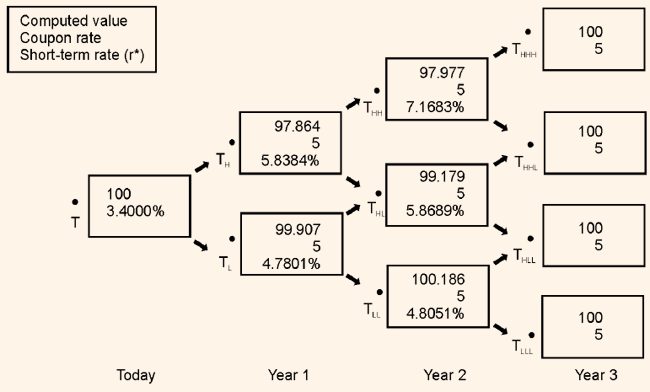
Assumed Volatility = 10%

Coupon tate = 5%