Compute the total capacitance with parallel connection:

Three capacitors C₁, C₂ and C₃ contain capacitance 20 μf, 15 μf, 30 μf, respectively. compute:

1. Charge on each of the capacitor when connected in parallel with 220 V supply.

2. Total capacitance with parallel connection.

3. Voltage across each of the capacitor when connected in series and 220 V supply is given to this series connection.

Solution

 (a) Capacitors are in parallel:

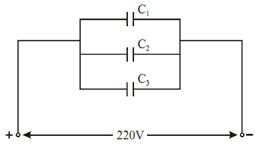
Figure

Q₁ = C₁ V = 20 × 10^-6  × 220 = 4400 × 10

Q₂ = C₂ V = 15 × 10^{- 6} × 220 = 3300 × 10^{- 6} C

Q₃  = C₃ V = 30 × 10^{- 6} × 220 = 6600 × 10^{- 6}  C

 (b)       Total capacitance :

      C = C₁ + C₂ + C₃

          = (20 + 15 + 30) × 10^{- 6}

           = 65 μF

(c) As capacitors are in series so charge Q remains same for all capacitors.

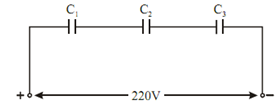
Figure

1 /C_eq      =  (1 / C₁ )+   (1 / C₂ ) +(1/C₃)

1 / C_eq =   1 /20  + 1/15 + 1/30  = 0.05 + 0.0666 + 0.0333

 C_eq = 6.667 μF

Total charge Q = C_eq × V

= 1466.74 μC

Now,    Voltage across C₁ is V₁ = Q/ C₁ = 73.337 volt

Voltage across C  is V   =  Q/ C₂ == 97.78 volt

Voltage across C  is V  =  Q/C₃  == 48.89 volt