Compute the coefficient of friction at block:

The frame shown in Figure rotates about a vertical axis. The coefficient of friction under block A is 0.4. Compute the coefficient of friction at block B if B starts to rise when the frame rotates at 40 rpm.

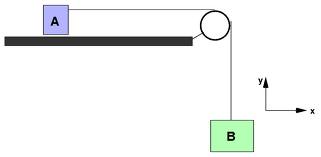
Solution

As the table rotates, block A shall try to move outwards.

We have,        ω = (40 × 2 π )/60

                       = 4.19 rad / sec

The acceleration acting on Block A towards axis of rotation shall be

r ω² = 21.06 m / sec²            (r = 1.2 m)

let FBD of Block A (Figure (b)), writing equilibrium equation, we have

T =   (100/g )  × a_n  - F

We get,

T = (100 /g) × a_n - 0.4 F₁

= (100 /9.81) × 21.06 - 0.4 × 100

= 174.67 N

Now considering FBD of Block B, (Figure (c)).

Figure 6.15(c)

We get,

T = 80 + (80 /9.81) × 21.06 × μ

 ∴ μ = (174.67 - 80)/171.74

= 0.55