These are the only possibilities for solving quadratic equations in standard form. However Note that if we begin with rational expression in the equation we might get different solution sets since we might have to ignore one of the possible solutions thus we don't get division by zero errors.
Now, it turns out that all we have to do is look at the quadratic equation (in standard form of course) to find out which of the three cases that we'll get. In order to see how this works let's begin by recalling the quadratic formula.
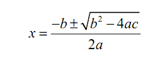
The quantity b2 - 4ac in the quadratic formula is called the discriminant. It is the value of the discriminant which will determine which solution set we will get. Let's go through the cases one at a time.
1. Two real distinct solutions. We will obtain this solution set if b2 - 4ac >0. In this case we will be taking square root of positive number & hence the square root will be a real number. Thus the numerator in the quadratic formula will be -b plus or minus a real number. It means that the numerator will be two different real numbers. Dividing either one through 2a won't vary the fact that they are real, nor will it vary the fact that they are distinct.
2. A double root. We will obtain this solution set if b2 - 4ac = 0 . Here we will be taking the square root of zero that is zero. Though, it means that the "plus or minus" part of the numerator will be zero and thus the numerator in the quadratic formula will be -b. In other terms, we will get a single real number out of the quadratic formula that is what we get while we get a double root.
3. Two complex solutions. We will obtain this solution set if b2 - 4ac < 0. If the discriminant is -ve we will be taking the square root of negative numbers in the quadratic formula that means that we will obtain complex solutions. Also, we will obtain two since they have "plus or minus" in front of the square root.
Hence, let's summarize up the results here.
1. If b2 - 4ac>0 then we will obtain two real solutions to the quadratic equation.
2. If b2 - 4ac = 0 then we will obtain a double root to the quadratic equation.
3. If b2 - 4ac <0
then we will obtain two complex solutions to the quadratic equation.