Calculate pressure on each side of spherical ball :

Heavy spherical ball of weight W rests in V shaped trough whose sides are inclined at the angles and to the horizontal. Find pressure on each side of trough. If second ball of equal weight be placed on side of inclination, so as to rest above the first, find pressure of the lower ball on side of inclination.

Sol.: Let

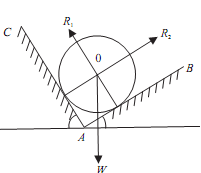
R₁  = Reaction of inclined plane AB on                                                       

the sphere or required pressure on AB                           

R₂  = Reaction of inclined plane AC on

the sphere or required pressure on AC

The O is in equilibrium under the action of

following three forces: W, R1, R2

Case - 1:

Apply lami's theorem at point O               

R₁/sinß = R₂/sin(180 -α  ) = W/sin(α   +β   )

or                       R1 = Wsinβ  /sin(α   +β   )           .......ANS                                            

and                     R2 = Wsinα  /sin(α                        + β  )                                             .......ANS        Fig 6.74

Case - 2: Let

R₃  = Reaction of inclined plane AC on the bottom sphere or required pressure on AC

As the two spheres are equal, the center line O1O2  is parallel to plane AB.

When the two spheres are considered as single unit, the action and reaction between them at the point of contact cancel each other. Considering equilibrium of the two spheres taken together and resolving the forces along Line O1O2, we get

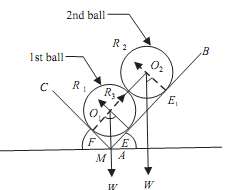
R3cos{90° - (α  +β   )} = Wsinα  + Wsinα

R₃sin(α + β ) = 2Wsinα

Or, R₃ = 2Wsin α /sin(α + β   )    .......ANS