Average Function Value

The average value of a function f(x) over the interval [a,b] is specified by,

f_avg = (1/b-a) _a∫^b f(x) dx

Proof

We know that the average value of n numbers is only the total of all the numbers divided with n therefore let's start off with this. Let's take the interval [a,b] and divide this in n subintervals each of length,

x = (b -a)/n

Now by all of these intervals select the points x₁*, x₂*,...., x_n* and consider that this doesn't really issue how we select each of these numbers as long as they arrive from the suitable interval.

 We can then calculate the average of the function values f(x₁*), f(x₂*),.....,f(x_n*) by computing,

(f(x₁*), f(x₂*),.....,f(x_n*))/n

Here, from our definition of ?x we can find the formula for n as given in below.

n = (b -a)/ ?x

and we can plug it  in (4) to have,

(f(x₁*), f(x₂*),.....,f(x_n*))/((b -a)/ ?x)

= ([f(x₁*), f(x₂*),.....,f(x_n*)]?x)/(b -a)

= (1/(b -a)) ([f(x₁*), f(x₂*),.....,f(x_n*)]?x)

= (1/(b -a)) 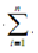     f(x_i*)?x

Let's here raise n. Doing that will mean that we are taking the average of increasingly function values in the interval and therefore the larger we select n the better it will approximate the average value of the function.

If we did so take the limit as n goes to infinity we must find the average function value. Or,

f_avg = lim_n→∞ (1/b-a) 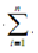        f(x_i*) ?x = (1/(b -a))  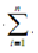                     _a∫^b f(x_i*) dx

We can factor the 1/(b -a) out of the limit where we have done and here the limit of the sum must look familiar as which is the definition of the definite integral. Therefore, putting in definite integral we find the formula as we were after.

f_avg = (1/(b -a)) _a∫^b f(x) dx