Q. In the given figure find the shortest path from A to Z using Dijkstra's Algorithm.
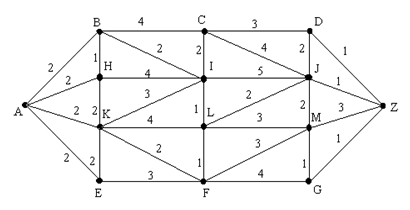
Ans:
1. P=φ; T={A,B,C,D,E,F,G,H,I,J,K,L,M,Z}
Let L(A)=0 and L(x)=∞ for all x in T ( L(x) denotes label of x)
2. P={A}, T={B,C,D,E,F,G,H,I,J,K,L,M,Z} A≠Z so calculate the new labels for vertices in T
|
L(B)=min(∞, 0+2)=2
|
L(H)=min(∞, 0+2)=2
|
|
L(C)=min(∞, 0+∞)=∞
|
L(I)=∞
|
|
L(D)=∞
|
L(J)=∞
|
|
L(E)=min(∞, 0+2)=2
|
L(K)=min(∞, 0+2)=2
|
|
L(F)=∞
|
L(L)=∞
|
|
L(G)=∞
|
L(M)= ∞ ; L(Z)= ∞
|
3. v=B, is the vertex with the smallest label, L(v)=2
P={A,B}, T={C,D,E,F,G,H,I,J,K,L,M,Z} B≠Z so calculate the new labels for vertices in T
|
L(C)=min(∞, 2+4)=6
|
L(I)=min(∞, 2+2)=4
|
|
L(D)=∞
|
L(J)=∞
|
|
L(E)=min(2,2+∞)=2
|
L(K)=min(2,2+∞)=2
|
|
L(F)=∞
|
L(L)=∞
|
|
L(G)=∞
|
L(M)=∞
|
|
L(H)=min(2,2+1)=2
|
L(Z)= ∞
|
4. v=E, vertex containing the smallest label, L(v)=2
P={A,B,E}, T={C,D,F,G,H,I,J,K,L,M,Z} B≠Z so calculate the new labels for vertices in T
|
L(C)=min(6, 2+∞)=6
|
L(J)= ∞
|
|
L(D)=∞
|
L(K)=min(2,2+2)=2
|
|
L(F)=min(∞,2+3)=5
|
|
|
L(G)=∞
|
L(L)=∞
|
|
L(H)=∞
|
L(M)=∞
|
|
L(I)= ∞
|
L(Z)= ∞
|
5. v=K, vertex containing the smallest label, L(v)=2
P={A,B,E,K}, T={C,D,F,G,H,I,J,L,M,Z} K≠Z so calculate the new labels for vertices in T
|
L(C)=min(6, 2+∞)=6
|
L(J)= ∞
|
|
L(D)=∞
|
L(L)=min(∞,2+4)=6
|
|
L(F)=min(5,2+2)=4
|
L(M)=∞
|
|
L(G)=∞
|
L(Z)= ∞
|
|
L(H)=min(∞,2+2)=4
|
|
|
L(I)= min(∞,2+3)=5
|
|
6. v=F, vertex containing the smallest label, L(v)=4
P={A,B,E,K,F}, T={C,D,G,H,I,J,L,M,Z} K≠Z so calculate the new labels for vertices in T
|
L(C)=min(6, 4+∞)=6
|
L(I)= min(5,4+∞)=5
|
|
L(D)=∞
|
L(L)=min(6,4+1)=5
|
|
L(G)=min(∞,4+4)=8
|
L(M)=min(∞,4+3)=7
|
|
L(G)=∞
|
L(Z)= ∞
|
|
L(H)=min(4,4+∞)=4
|
L(J)= ∞
|
7. v=H, vertex containing the smallest label, L(v)=4
P={A,B,E,K,F,H}, T={C,D,G,I,J,L,M,Z}
K≠Z so calculate the new labels for vertices in T
|
L(C)=min(6, 4+∞)=6
|
L(J)= min(∞,4+∞)=∞
|
|
L(D)=∞
|
L(L)=min(5,4+∞)=5
|
|
L(G)=min(8,4+∞)=8
|
L(M)=min(7,4+∞)=7
|
|
L(I)=min(5,4+4)=5
|
L(Z)= ∞
|
8. v=I, vertex containing the smallest label, L(v)=5
P={A,B,E,K,F,H,I}, T={C,D,G,J,L,M,Z} I≠Z so calculate the new labels for vertices in T
|
L(C)=min(6, 5+2)=6
|
L(L)= min(5,5+1)=5
|
|
L(D)=∞
|
L(M)=min(7,5+∞)=7
|
|
L(G)=min(8,5+∞)=8
|
L(Z)=∞
|
|
L(J)=min(∞,5+5)=10
|
|
9. v=L, vertex containing the smallest label, L(v)=5
P={A,B,E,K,F,H,I,L}, T={C,D,G,J,M,Z}
L≠Z so calculate the new labels for vertices in T
|
L(C)=min(6, 5+∞)=6
|
L(J)= min(10,5+2)=7
|
|
L(D)=∞
|
L(M)=min(7,5+3)=7
|
|
L(G)=min(8,5+∞)=8
|
L(Z)=∞
|
10. v=C, vertex containing the smallest label, L(v)=6
P={A,B,E,K,F,H,I,L,C}, T={D,G,J,M,Z} C≠Z so calculate the new labels for vertices in T
|
L(D)=min(∞,6+3)=9
|
L(M)= min(7,6+∞)=7
|
|
L(G)=min(8,6+∞)=8
|
L(Z)=∞
|
|
L(J)=min(7,6+4)=7
|
|
11. v=J, vertex containing the smallest label, L(v)=7
P={A,B,E,K,F,H,I,L,C,J}, T={D,G,M,Z} J≠Z so calculate the new labels for vertices in T
|
L(D)=min(9,7+2)=9
|
L(M)= min(7,7+2)=7
|
|
L(G)=min(8,7+∞)=8
|
L(Z)=min(∞,7+1)=8
|
12. v=M, vertex containing the smallest label, L(v)=7
P={A,B,E,K,F,H,I,L,C,J,M}, T={D,G,Z} M≠Z so calculate the new labels for vertices in T
|
L(D)=min(9,7+∞)=9
|
L(Z)= min(8,7+3)=8
|
|
L(G)=min(8,7+1)=8
|
|
13. v=G, vertex containing the smallest label, L(v)=8
P={A,B,E,K,F,H,I,L,C,J,M,G}, T={D,Z}
G≠Z so calculate the new labels for vertices in T L(D)=min(9,8+∞)=9 L(Z)= min(8,8+1)=8
14. v=z, so now we stop here, the Shortest distance is 8
Backtracking all the steps we get, shortest path as: A-K-F-L-J-Z