Reference no: EM131057630

Question 1: 

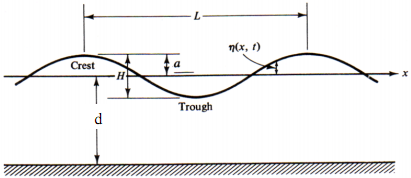
A wave with the deep-water characteristics of (T = 6.8 s and H = 5.0 m) is propagating toward a coast, where the water depth is 6.2 meters. At the coast, the surface elevation can be described as

η(t) = (H/2) cos(ω/t), and

the horizontal and vertical water particle velocities of the wave can be calculated with

u(t) = (ωH/2)(cosh(k(z+d))/sinh(kd))cos(ωt)

v(t) = -(ωH/2)(sinh(k+(z+d))/sinh(kd))sin(ωt)

where g is the gravity, H is the wave amplitude, k is the wave number, d is the mean water depth, ω is the angular frequency, z is the location below the mean water level (MWL).

Write MATLAB codes to-

(i) Determine the wave characteristics (i.e. wave height, wave length, wave number, wave celerity) in deep water and at the coast (use the Dispersion relationship and fzero function in MATLAB);

(ii) Calculate the horizontal and vertical water particle velocities for t varies for 2 wave periods and z varies from 0 to -d (with an interval of 1 m).

(iii) Generate figures to present the time series (t varies from 0 to 2T) of the water particle velocities at the locations of the trough, z = -H/2 m and at the bottom. (iii) present the vertical profile of the magnitude of horizontal water particle velocity from the MWL to the sea bottom.

(iv) generate a similar graph as below for one wave period and at the mean  water level, to show the relationship between the surface elevation, the horizontal and vertical  water particle velocities.

Question 2-

Consider a 5km stretch of coast oriented in the north-south direction with the ocean to the east. The predominant wave direction is from the east-south-east. At the southern end the typical breaker height is 1.4 m and the breaker angle is 10^o. At the northern end, the breaker height is 1.45m and the breaker angle is 12^o. The breaker parameter γ_b = 0.8.

The beach profiles along the section are similar with slopes near the break point of 1/40. The sand is made of quartz (s = 2.63, p = 0.28) with a median grain size of 0.22mm and measureable seasonal bed level changes are restricted to depths less than 6 metres. The berm height is 3 m AHD.

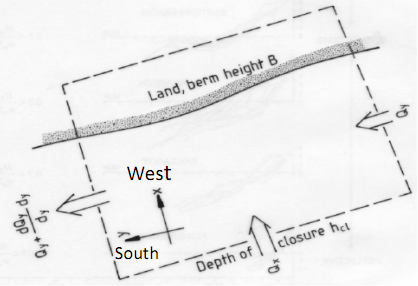
The average shorenormal sediment transport rates (Q_x) for 1993-2015 were saved in the data file "sediment.xlsm". There are no sinks and sources for sediment transport in the control domain. The erosion rate (metres of shoreline retreat rate) can be calculated using (see details in Coastal Process module lecture notes)

(1-p)(h_c + B) ∂x_s/∂t = -Q_x + ∂Q_y/∂y + Q_sink - Q_source

Q_y = (K/16(s-1)√γ) √gH_b^5/2 sin2θ_b

where

p is the sediment porosity,

x_s is the shoreline coordinate

Q_source is a sediment input (e.g. river discharge, beach nourishment)

Q_sink is a sediment loss (e.g. dredging)

K ≈ 0.77 is an empirical coefficient which has a weak dependence on grain size.

s is the specific weight

H_b is the breaker height

γ is the breaker index

θ_b is the wave crest angle at the break point

all other variables are as defined in the figure.

The aerial photographs of the stretch of the coast from 1993 to 2015 indicate the shoreline location, x_s which were saved in the file "shoreline.xlsm".

Use Matlab to develop a numerical model to calculate the location of the shoreline from 1993 to 2015, i.e. xs. (assume x_s = 0 in 1993)  Evaluate the accuracy of the model.

Attachment:- Assignment.rar