Reference no: EM13913215

Assignment- Computational and Experimental Methods: Computational

a) The Steady-State Heat Diffusion Equation

Consider steady state heat diffusion in the following domain:

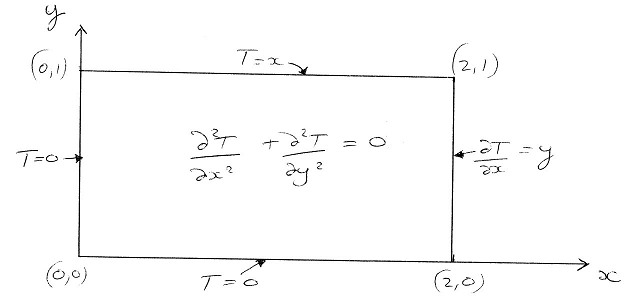
The boundary conditions for this problem are:

- T = 0 for x = 0, 0≤y≤1

- T = 0 for y = 0, 0≤x≤2

- T = x for y = 1, 0≤x≤2

- ∂T/∂x=y for x = 2, 0≤y≤1

Consider the following Finite Difference mesh with N=4 internal nodes in the vertical direction and a total of 10 nodes (including at x=2) in the horizontal direction. In all cases you will consider here, you will use the same uniform grid spacing in the x and  y directions. This means that if N is the number of internal nodes in the vertical direction then the number of nodes in the horizontal direction is 2(N+1). In the example shown below this leads to a grid spacing Δ = Δx = Δy = 0.2

The  node  numbering  scheme  to  be  used  is  shown  above  where Ti indicates the unknown temperature at node i. As in the relevant section of the notes, you will need to introduce "ghost" nodes outside the domain in order to apply the Finite Difference form of the heat diffusion equation

(∂²T/∂x²)+(∂T/∂y²)=0

at the boundary  nodes T10, T20, T30 and T40 and  a second  order,  central difference approximation  to the  boundary condition ∂T/∂x=y at x=2 in order to eliminate the ghost nodes from the Finite Difference equations.

Write a Matlab M-code program which solves the Finite Difference equations for the unknown temperatures T_i where the value of N, the number of internal nodes in the vertical direction, is specified as a parameter at the beginning of the program. Your program should also do the following.

-Write the numerical values of temperature and the corresponding value of the analytical solution to this problem, T = x y , at each of your grid points, to a text file.

- Calculate the maximum percentage difference between your numerical solution and the analytical solution in the form [100 (numerical - analytical)/analytical] over all the grid points and write this value to the same text file to which you have written the numerical and analytical results.

You are asked to hand in the following:

(i)  A copy of your Matlab M-code program, which is documented similarly to the programs you have been given during the lectures, together with your results file for the case with N=4, which show the numerical and analytical values at each grid point and which contains the maximum percentage difference between the analytical and numerical solution over the entire grid of 40 points.

(ii)  A sheet on which you have derived (i.e. do not simply write them down) the Finite Difference equations for the above grid with N=4 (and a total of 40 unknowns) at nodes 1 and 40.

(iii)   Generate a 3-D plot of the temperature against x and y including the boundary values, e.g. using the Matlab function surf.

When writing your program you may find it useful to populate your temperature matrix by considering the equations at the following nodes separately:

i. All nodes not influenced by the boundary conditions, i.e. those not  adjacent to the boundaries.

ii. Each of the four corner nodes separately

iii. Nodes adjacent to the bottom (y=0) boundary but not at the corners

iv. Nodes adjacent to the left boundary (x=0) but not at the corners

v. Nodes adjacent to the upper boundary (y=1) but not at the corners.

vi. Nodes on the right hand boundary (x=2) but not at the corners.

Note that for the grid given above these different sections would be

i. Nodes 12-19, 22-29.

ii. Nodes 1, 10, 31, 40

iii. Nodes 2-9

iv. Nodes 11, 21

v. Nodes 32-39.

vi. Nodes 20, 30.

b) A Parabolic Partial Differential Equation

In   this   question   you   will   solve   the   time-dependent   heat   diffusion   equation π²∂T/∂t=∂²T/∂x² over the region 0≤x≤1, 0≤t≤10 subject  to  the boundary conditions T (x,0) = sin πx and T (0, t) =T (1, t) = 0.

(i) By modifying the program tdepheat_theta.m for the general θ method, write a Matlab program that solves this equation numerically using the θ method with N evenly spaced nodes in the x direction (node 1 is at x=0 and node N is at x=1) and Nt evenly spaced time points in the time direction (time node 1 corresponds to t=0 and node Nt is at t=10). In this case the grid spacing in the x direction is 1/(N-1) and the time step is 10/(Nt-1). Your program should also plot out your numerical solution at t=10 for 0≤x≤1. Hand in a copy of your program, highlighting the modifications to Tdepheat_Theta.m that you have made to solve this problem.

(ii) Use your program to plot out your numerical solution at t=10 for the following parameters:

(a) θ=0.5 (Crank-Nicolson) with N=11 and Nt=181.

(b) θ=1.0 (Backward Euler) with N=11 and Nt=181.

(c) θ= 0.0 (Forward-Euler) with N=11 and determine the approximate value for Nt at which this approach becomes stable.

For each set of parameters, hand in hard copies of your graphs. Hence or otherwise discuss the stability of the solutions with the 3 methods.

c) A Hyperbolic Partial Differential Equation

In this question you will solve the simple wave equation 4∂²y/∂t²=∂²y/∂x² in the region 0≤x≤1, t=0 subject to the initial conditions y(x,0)=f (x) = 0 and ∂y/∂t(x,0) = g( x) = sin(2πx) at t=0. You are also given that y(0,t) = y(1,t) = 0 for all t.

Write a Matlab program which solves this equation using finite differences. The boundary conditions for this problem represent a higher order vibration mode in comparison to the exercise covered in the notes, as defined by the initial condition for the velocity.

Your program should use a definition for Nx (the number of uniformly spaced nodes in the x direction including the two boundary nodes at x=0 and x=1) and calculate the time step to apply on the basis that ??? = ???/c. Nt (the number of time steps) should be setup to show at least 1.5 full oscillations of the wave. You should generate solutions based on equation 8 and equation 15 (in the notes) to define the initial conditions.

You should also generate an analytical solution based on the application of D'Alembert's method, equation 12. The output should include a 3-D figure (e.g. using surf) of the solution obtained using finite differences and equation 15. You should also generate a plot which shows  the accuracy of the two methods in comparison to the analytical solution, e.g. by plotting y1(round(Nx/4),:).

You are asked to hand in the following:

a) A copy of your program with brief explanatory comments

b) A graph of the results and comparison of D'Alembert and the two finite difference approaches with Nx = 21, or equivalently Dx = 0.05.

Attachment:- Tdepheat_Theta.m