Reference no: EM13692991

EXERCISE 1: REGULAR EXPRESSIONS

Question 1. Let R₁ = a((b*c*) + a)b and R₂ = a* ((bc) + a*)b* be two regular expressions.

(a) Give two words ω₁ and ω₂ such that {ω₁ ω₂} ⊆ L(R₁) ∩ L(R₂). Please type each word on a new line.

(b) Give two words ω₃ and ω₄ such that (ω_3, ω₄) ⊆ L(R₁) \ L(R₂). Please type each word on a new line.

(c) Give two words ω₅ and ω₆ such that {ω₅, ω₆} ⊆ L(R₂) \ L(R₁). Please type each word on a new line.

(d) Give a regular expression R₃ such that L(R₃) = L(R₁) U L(R₂).

(e) Give a regular expression R₄ such that L(R₄) = L(R₁) ∩ L(R₂).

Question 2. Give regular expressions for the following languages.

(a) L₁ = {aⁿb^m | n ≥ 3, m is even}.

(b) L₂ = L₁' (where L' stands for the complement of L).

(c) L₃ = {abⁿω | n > 3, ω  ∈ {a, b}*}.

(d) L₄ = {ωaⁿω | n > 0, ω ∈ {a, b}*} ∩ {bωb | ∈ {a, c}*}.

Question 3. Let R₁ and R₂ be regular expressions over a non-empty alphabet E.

(a) Determine, formally, whether L(R₁(R₁ + R₂)*) = L((R₁ + R₂)*). That is, if it is true, provide a proof; otherwise provide a counter example.

(b) Prove that L(R₁R₂)^Τ = L(R^Τ₂, R₂)*) where if represents the reverse of regular expression R. For example, if abb ∈ L(R), then bba ∈ L(R'). Similarly, if X is a set of words, then X^Τ = {ω|ω^r ∈ X}.

EXERCISE 2: GRAMMARS

Question 4. In this exercise, we use operator R# to denote one or more repetitions of R, that is, R# is a compact way of writing RR' (remember we used + for alternation). Let L₁ and L₂ be the following two languages over alphabet {a, b, c}:

L₁ = {aⁿb²c^m a^2+n+m | n,m ≥ 1};

L₂ = L(((a + b)*b(b + (c + a) (b + a)* )#.

(a) Give a grammar G₁ such that L(G₁) = L₁.

(b) Give a grammar G₂ such that L(G₂) = L₂.

(c) Provide a grammar G₃ such that L(G₃) = L₁ U L₂.

(d) Prove formally that L₁ ∩ L₂ = L₁

Question 5. Let G = ({S, A}, {a, b}, Γ, S) be a grammar, where the set of rules r is defined as follows:

S -> aSbS
S -> bSaS

S -> ∈

(a) Is G an ambiguous grammar? Explain your answer.

(b) Is there a relationship between the number of a's and b's in L(G)?

(c) Does there exist a regular expression R such that L(R) = L(G)? If it exists, provide such R; otherwise, briefly explain the reason for its nonexistence.

(d) Does there exist a regular expression, DFA, or PDA over the alphabet Σ = {a, b} which is equivalent to the language L₁ = L(G) ∩ L(a*b*)? For each, briefly explain why not or provide the expression/automaton.

EXERCISE 3: AUTOMATA
Question 6. Answer the following questions based on the finite state automaton M₁ present in the JFLAP file DFA-3.6.jff available in Course Material section of the course website.
 
(a) Give four strings of length 3 accepted by M₁. Please type each string on a new line.
(b) Give four strings of length 3 rejected by M₁. Please type each string on a new line.
(c) Do you think M₁ has more states than required to express its language? Explain briefly.
(d) Give the language of this machine M₁ as a regular expression.
(e) Create an automaton M₂ such that it accepts the language L₂ where L₂ = L(M₁) ∩ L(a*c*(c+ b)*). Your machine should not accept words not in this language.
 
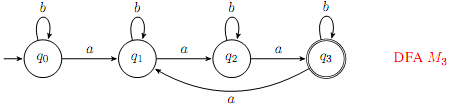
Question 7. Let M₃ = ({q₀, q₁, q₂, q₃}, {a, b} , δ, q₀, {q₃}) be a deterministic finite state machine as shown below. Prove that if w is a string in L(M₃), then the number of a's in ω is n_a,(ω) mod 3 = O.

Question 8. Consider the pushdown automaton M₄ over the alphabet Σ = {a, b, c} as shown below.

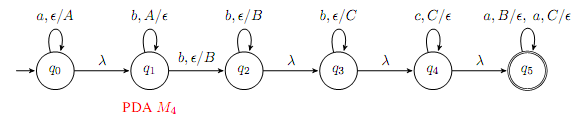
Notation x, A/X means a transition where X is the input symbol being read, A is the symbol on top of the stack that is popped, and X is the symbol pushed onto the stack. The symbol ∈ stands for the "empty" string. Acceptance is by final state and empty stack.
 
(a) Give 4 strings of length 6 over Σ that are accepted by PDA M₄.
(b) Give 4 strings of length 6 over Σ that are rejected by PDA M₄.
(c) Give the language of M₄ in set notation.
(d) Let M₅ be a PDA obtained from M₄ by removing the transitions δ(q₄, ∈, ∈) = (q₅, ∈), δ(q₅, a, B) = (q₅, ∈) and δ(q₅, a, C) = (q₅, ∈), adding transition δ(q₄, a, B) = (q₄, ∈), removing state q₅ and making state q₄ a final state. Give the language of M₅ in set notation.

(e) Is there a relation between the language of M₄ and M₅. Explain briefly.

(f) It is a well known result that every PDA with acceptance condition of an empty stack and reachability of a final state can be transformed to an equivalent PDA with acceptance condition requiring only reachability of a final state. Transform the PDA M₄ to an equivalent PDA with acceptance requiring only reachability of a final state.