Function: A function from A to B is a relation A × B such that no two different ordered pairs of the relation have the same first component and every element of A has an image in B.
It is denoted by f : A → B·
or A 1→ B.
DOMAIN, RANGE AND CO-DOMAIN OF FUNCTION
Domain: Domain of a function is the set of values of x, when (x, y) belongs to the function.
Range: Range of a function is the set of value of y, when (x, y) belongs to the function.
Co-domain: If (x, y) belong to a function f : A → B then Y is called codomain of the function. Range is a subset of co-domain sometimes the range and co-domain have the same elements.
Note:
(i) Each element of the set A must be associated.
(ii) All the elements of the set B neednot have the association
(iii) 'The set of elements of B which are associated is called the 'range' of the function.
(iv) The range will be subset of the co-domain.
Kinds of functions:
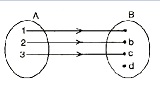
(1) The function f: A → B is called an into function, if there is at least one element of set B which has no pre-image in set A.
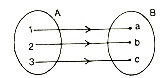
(2) The function f: A → B is called an onto function if every element of set B has at least one pre-image in set A.
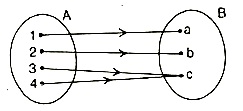
(3) The function f: A → B is called one-one if distinct elements have distinct images.
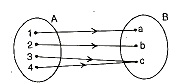
(4) The function f: A → B is called many-to-one, if one or more elements of set A there correspond only one element of set B.
Note:
(1) One-one is also written as 1 - 1.
(2) An onto function is also called 'surjection'.
(3) A1 - 1 onto function is called a 'bijection'.
Representation of a function: A function may be indicated by:
(i) a verbal description
(ii) an arrow diagram
(iii) a tabular form
The table represents a function.
X 0 1 2 3
Y 1 4 5 7
(iv) A formula (called an equation).
The equation y = 2x + 3 represents a function.
(v) Set builder notation, such as f: {(x, y): y = 2x + 3)
Testing for function: It can tested whether a given relation is a function or not by using the following tests:
(i) In case of a function, the first set i.e., the domain is fully used up.
(ii) In case of a function, the first members of all the ordered pairs are different.
(iii) In case of a function, each element of the first set has only one image in the second set.
(iv) In case of function, a vertical line will intersect the graph of the function at one point only as shown below:
Functions and Kinds of Functions, Math Homework Help, Assignment Help
Are you struggling with functions and kind of functions related math problems? Does your child need help with tutor to complete his homework? Expertsmind.com helps to finish your child homework by quick assistance of qualified math tutors. We at Expertsmind.com offers math homework help, math assignment help and solutions by best online support for 24 * 7 hours. Our tutors are helping students in solving their doubts and problems during their studies. Get solved functions and kind of functions homework problems with step by step answers.