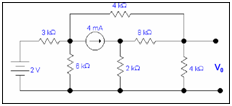
Q:  Find out the value of voltage V_o by using Norton's theorem .

Sol:

We have to calculate V₀  by using Norton's theorem.

Step 1:  Replacing R_L with a short circuit to search I_N. Here R_L is equal to 4k resistor.

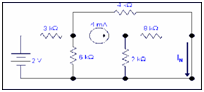
Step 2:

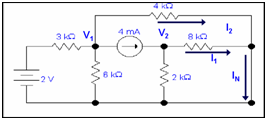
                                                            I_sc =I₁ + I₂

                        Apply KVL for node 1

                                                V₁/4k + (V₁ - 2)/3k + V₁/6k +4m=0

                                                            3V₁ +4V₁ - 8 +2V₁ +48 =0

                                                                         9V₁+40=0

                                                                        V₁= 4.44Volts

                        Now for node 2

                                                                        V₂/2k + V₂/8k -4 =0

                                                                   4V₂ +V₂ - 32 =0

                                                                          5kV₂ = 32

                                                                              V₂ =32/5 =6.4V

                        Now from the circuit we can say

                                                                         I₁ = V₂/8k

                                                                                         = 6.4/8k

                                                                        I₁ = 0.8 mA

                                                                        I₂ = V₁/4k

                                                                            = 4.44/4k    =1.11mA

                        Therefore,

                                                             I_N = I₁+ I₂

                                                             I_N = (1.11 + 0.8) = 1.91mA

Step 3: Determining R_N

To compute R_N we short circuit all of voltage sources and open the current sources.

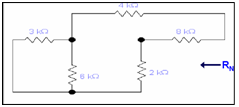
For R_N

                                                  3k|| 6k = 2k

                                           2k is in series through 4k = 2k + 4k= 6k

                                           8k is in series with 2k = 8k + 2k=10k

                                                10k ||6k = 10 x6/16

                                                              =60/16 =3.75k

Step 4:

After determining I_N & R_N, re-inserting the load resistance R_L in the circuit in parallel R_N and letting the I_N current source parallel along these two resistances.

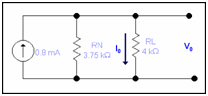
                        To find out V₀

                                                 I₀ = 1.91m x 3.75k x 1/(4k+3.75k) = 0.92mA

                                                  V₀ = 4k x 0.92m=3.68 Volts