Second period diatomics

In expanding the MO  theory to second period elements two additional principles require to be considered. First, only valence-shell orbitals are displayed in MO  diagrams,  as the inner shells are too tightly bound  to be involved  in bonding and do not overlap considerably. Second, both 2p and 2s valence orbitals require to be included. The three AOs inside a p shell different only in their direction in space, and in an atom are degenerate (that is have similar energy). Though, in diatomic molecules, they are differentiated by the way they overlap: pσ orbitals point along the direction of the bond and pπ orbitals (of which there are two degenerate and equivalents ones) are perpendicular to it. Every type of orbital can merge to form MOs  in similar way as in H₂. Two basic rules in the LCAO  MO model are significant:

1. The no. Of MO_s formed is equal to the total number of starting AO_s;
2. Only AO_s of similar symmetry type combine to make MO_s.

Figure 3 depicts that the pσ AO_s,  which point in the direction of each other, overlap more strongly than do pπ MO_s,  so that both the antibonding destabilization and the bonding stabilization is greater for pσ. The order of MO energies generated from the 2p AO on the two atoms is so:

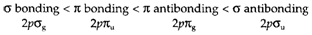
The symmetry designation of every MO is given and it should be noticed that the g or u labeling for π MO_s  is the opposite of that for σ MO_s.

Figure 4 depicts the MO diagram for dioxygen O₂. Like in Fig. 2 the energies of 2s and 2p AO_s of the separate atoms are displayed and among them the MO_s formed from overlap. Lowest in energy are 2_sσ_g and 2_sσ_u, correspondingly the bonding and antibonding combinations of 2_s AO_s. At the higher energies are MOs  resulting from 2p AO_s. Figure 4 depicts occupation of MOs in O₂ (12 valence electrons). The BO considered as above is two, as supposed from the normal valence structure.  Though,  the degenerate 2_pπ_g MOs  are occupied by two electrons and like in atoms, Hand's first rule depicts that the ground  state will  be created  by putting  one electron in each orbital with  parallel spin. So O₂ is correctly predicted to have two unpaired electrons and as a consequence is paramagnetic.

One of the benefit of MO  theory is that similar diagram can be employed for molecules with distinct numbers of electrons. The electron configurations and the BO_s for some molecules and ions, that can be derived using Fig. 4. are displayed in Table 1 together with the experimental bond lengths and dissociation energies. Higher predicted BO values correspond to shorter and stronger bonds.

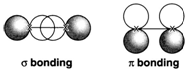
Diagram 3. Bonding MOs formed by σ and π overlap of 2p AO_s. Negative regions of the wave function are shaded.

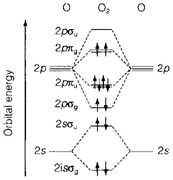
For more sophisticated reasons (example interpretation of molecular spectra) a number of refinements require to make to this simple picture. Particularly, the possibility of overlap between a 2s orbital on one atom and the 2pσ on the other can change the order of MO energies. This does not change the electron configurations  of any species displayed in Table 1. but is significant  for some molecules like C₂ (known at high temperatures, example in flames) and for heteronuclear molecules

Table 1. Electron configurations, bond orders (BO), dissociation energies (D) and bond lengths (R) for some homonuclear diatomics