Bonding and antibonding orbitals

Just like an atomic orbital (AO) is the wave function for an electron in an atom so a molecular orbital (MO) is that for a molecule; an MO may expand over two or more atoms. Correct MOs may be obtained by solution of Schrödinger's equation for the one-electron ion   but like in atoms the extension of the orbital approach to several- electron systems involves approximations. For MOs  a further approximation  is frequently made: rather than using the  correct but  very complicated  wave function  for H₂⁺   it  is convenient  to  express each MO like  a  linear combination of AOs, so-called LCAO approximation. This approximation requires being refined significantly for quantitative calculations on computers but it is sufficient for qualitative purposes and provides very helpful pictures of how chemical bonds form, and how they are associated to the valence AOs of the atoms involved.  

Diagram 1 depicts how the LCAO method works for H₂. The diagrams depict how the value of a wavefunction changes along the molecular axis. Figure 1a displays wavefunctions and Φ₁ for Φ₂ the 1s valence AOs on the two H atoms. An MO wave function ψ is constructed by writing

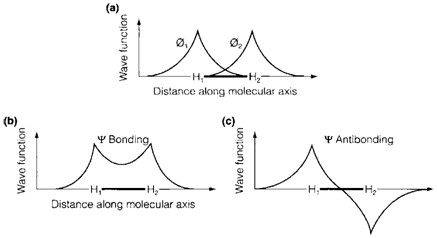
Fig. 1. Formation of a bonding and antibonding MO from the overlap of 1_s AOs in H₂ (see text)

In which c₁  and c₂  are numerical  coefficients.  The square of ψ gives the electron probability distribution, and in a homonuclear diatomic like H₂  (where each atom is similar) ψ2 must have similar value on each atom. So we have  from which either c₁=c₂ or c₁=-c₂. The previous combination is the bonding MO, and the later the antibonding MO, displayed in Fig. 1b and c. correspondingly. Almost each atomic nucleus both MOs resemble the 1_s AO (except sign, which does not influence the probability distribution). An electron that is close to one nucleus is hardly influenced by the existence of the other one. The significant variation takes place in the region among the nuclei, in which the bonding MO predicts an increase of electron density compared with the isolated atoms. This may be seen from the below equation

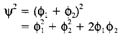
The first two  terms  give similar electron  density  as found  in the two 1_s AO_s, where   shows an increase of density in the region between the two atoms where the orbitals overlap. In the bonding an electron MO has lower energy than in the AO of an isolated atom, as it has improved probability of being close to both nuclei concurrently. The electrostatic repulsion among the nuclei is effectively shielded, leading to a stable bond.  Alternatively, in an antibonding MO an electron has higher energy, with a reduced possibility of being in the internuclear region and internuclear repulsion being 'deshielded'.

In the ground state of H₂ two electrons take place the bonding MO, the antibonding one not being employed. So, the simple MO model depicts how bonding arises from an increase of electron density in the internuclear region and how overlap of AO_s is necessary for this to happen.