Iterative Methods:
Apart from the non-interative methods mentioned above, there are a Ew iterative methods of obtaining p. These are discussed below.
The Cochrane-Orcutt method
This method starts with an initial estimate of ρ, the most convenient being 0, and the OLS estimates of β1 and β2 from (7.3), since we have assumed that ρ = 0. Note that if we start with an assumption other than ρ= 0 then we need to use equation (7.20) and not (7.3). Once we have the OLS estimates we can calculate the residuals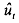
, also. Then we rum the same regression as in (7.22) above. The resulting estimate of p is
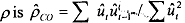where both summations run over t=2,3, ..., T since one observation is lost due to lags. The second step of the Cochrane-Orcutt method is to perform the regression in (7.20) with 6, instead of ρ. We can also iterate this procedure by computing new residuals based on the new estimates of 4 and 4 from (7.20), which are then used to calculate a new value of 
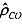, and so on until convergence takes place. It means that successive values of the ρ that is estimated do not change substantially, say the difference is less than 0.0 1.