Since we are going to be working almost exclusively along with systems of equations wherein the number of unknowns equals the number of equations we will confine our review to these types of systems.

All of what we will be doing now can be easily extended to systems along with more unknowns more equations than unknowns if require be.

 Let's begin with the subsequent system of n equations with the n unknowns, x₁, x₂,..., x_n.

a₁₁ x₁ + a₁₂ x₂ +................+a_1n x_n = b₁

a₂₁ x₁ + a₂₂ x₂ +.............. +a_2n x_n  = b₂

...................

a_n1 x₁ + a_n2 x₂ +............... +a_nn x_n  = b_n                              ...................(1)

Remember that in the subscripts on the coefficients for this system, a_ij, the i corresponds to the equation which the coefficient is in and the j corresponds to the unknown which is multiplied via the coefficient.

To utilize linear algebra to solve this system we will initially write down the augmented matrix for such system. An augmented matrix is actually just each the coefficients of the system and the numbers for the right side of the system written into matrix form. Now there is the augmented matrix in this system is,

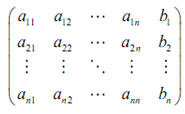
For solve this system we will utilize elementary row operations that we'll define these in a bit to rewrite the augmented matrix into triangular form. There is the matrix will be in triangular form if all the entries below the major diagonal there is diagonal containing a₁₁, a₂₂, ...,a_nn, are zeroes.

Once it is done we can recall that all rows in the augmented matrix correspond to an equation. We will after that convert our new augmented matrix goes back to equations and at such point solving the system will turn into very easy.

Before working an illustration let's first describe the elementary row operations. There are three of them.

1.   Interchange two rows. It is exactly what this says. We will interchange row i along with row j. The fact that we'll use to denote such operation is: R_i  ↔ R_j

2.   Multiply row i with a constant, c. it means that all entry in row i will get multiplied with the constant c. The fact for this operation is: cR_i

3.   Add a multiply of row i to row j.  Inside our heads we will multiply row i with an suitable constant and after that add the results to row j and place the new row back in row j leaving row i in the matrix unchanged. The fact for this operation is: cR_i + R_j

It's all the time a little easier to know these operations if we see them in action.  Therefore, let's solve a couple of systems.