Solve the subsequent differential equation and find out the interval of validity for the solution.

Let's start things off along with a fairly simple illustration so we can notice the process without getting lost in details of the other matters that frequently arise along with these problems.

dy/dt = 6 y²x, y(1) = 1/25

Solution:

This is clear, hopefully, as this differential equation is separable. Thus, let's divide the differential equation and then integrate both sides. As with the linear first order officially we will raise up a constant of integration on both sides from the integrals on every side of the equal sign. The two can be shifted to the similar side and absorbed in each other.  We will utilize the convention as puts the particular constant on the side along with the x's.

y^-2 dy = 6x dx

∫ y^-2 dy = ∫6x dx

-1/y = 3x² + c

Therefore, we now have an implicit solution. This type of solution is easy sufficient to get an explicit solution, though before getting that this is generally easier to get the value of the constant at such point. Therefore apply the initial condition and get the value of c.

-1/(1/125) = 3(1)² + c; c = -28

Plug this in the general solution and after that solves to find an explicit solution.

-1/y = 3x² + 28

y(x) = 1/(28 - 3x²)

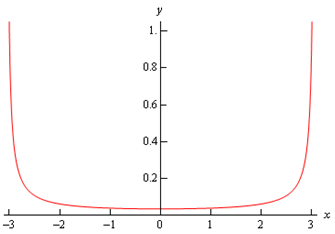
Here, as far as solutions go we have found the solution.  We do require starting worrying regarding intervals of validity however.

Recall as there are two conditions which describe an interval of validity.  First, it should be a continuous interval along with no holes or breaks in it.  Second it should include the value of the independent variable in the first condition, x = 1 in this instance.

Thus, for our case we've got to ignore two values of x that are:

x ≠ + √(28/3) ≈ + 3.05505

 These will provide us division via zero. This provides us three possible intervals of validity.

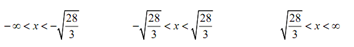
Though, only one of these will include the value of x from the initial condition and thus we can notice that

- √(28/3) < x< √(28/3)

It must be the interval of validity for such solution. Now is a graph of the solution.

Keep in mind that this does not as that either of another two intervals listed above cannot be the interval of validity for any solution. So along with the proper initial condition either of these could have been the interval of validity.

We will leave this to you to verify the details of the subsequent claims.  If we utilize an initial condition of

y(-4) = -1/20

We will find exactly the similar solution through in this case the interval of validity would be the individual.

- ∞ < x< -√(28/3)

Similarly, if we use

y(6) = -1/80

Since the initial condition we again find exactly similar solution and in this case the third interval turns into the interval of validity.

-√(28/3) < x < ∞

Thus, simply changing the initial condition a little can provide any of the possible intervals.