Solve 4 cos(t )= 3 on[-8,10].

Solution :Here the first step is identical to the problems in the previous section. First we need to isolate the cosine on one side by itself & then use our calculator to obtain the first answer.

cos(t )= 3/4      ⇒t = cos^-1( 3 )= 0.7227

Thus, this is the one we were by using above in the opening conversation of this section. At the time we specified that there were infinite number of answers & that we'd be seeing how to determine them later on. Well that time is now.

Firstly, let's take a rapid look at a unit circle for this example.

The angle which we've found is illustrated on the circle in addition to the other angle that we know has to also be an answer.  Determine this angle here is just as simple as in the previous section.  Since the line segment in the first quadrant forms an angle of 0.7227 radians with the +ve x-axis then so does the line segment in the fourth quadrant. It means that we can employ either -0.7227 as the second angle or 2π - 0.7227 =5.5605 .  Which you utilizes depends on which one you prefer.  We'll pretty much always utilize the positive angle to ignore the possibility that we'll lose the minus sign.

Thus, all possible solutions, avoiding the interval for a second, are then,

t = 0.7227+ 2π n

t = 5.5605 + 2π n

n = 0, ±1, ±2,.........

Now, all we have to do is plug in values of n to find out the angle that are really in the interval.  Following the work for that.

n = -2 :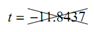     and            -7.0059

n = -1 :t = -5.5605       and              -0.7227

n = 0    :           t = 0.7227        and   5.5605

n = 1                :  t = 7.0059     and   11.8437

Thus, the solutions to this equation, in the following interval, are,

t = -7.0059, - 5.5605,- 0.7227, 0.7227, 5.5605, 7.0059

Note that we had anoption of angles to utilize for the second angle in the previous example.  The option of angles there will also affect the value(s) of n that we'll have to use to get all the solutions.  In the ending, regardless of the angle selected, we'll get the similar list of solutions;however the value(s) of n that gives the solutions will be different based on our choice.

Also, in the above instance we put in a little more explanation than we'll illustrates in the remaining examples in this section to remind you how these work.