Odd-Even Merging Circuit

Let's firstly understand the idea of merging two sorted sequences using an odd-even merging circuit. The functioning of a merging circuit is as given below:

 1)  Let there be 2 sorted sequences A= (a₁, a₂, a₃, a₄......... a_m) and B= (b₁, b₂, b₃, b₄......... b_m) that are needed to be merged. 

2)  With help of a merging circuit (m/2, m/2) merge the odd indexed numbers of two sub sequences it implies that (a₁, a₃, a₅......... a_m-1) and (b₁, b₃, b₅......... b_m-1) and so resulting in sorted sequence (c₁, c₂, c₃......... c_m).

3) Afterwards, with the help of a merging circuit (m/2, m/2) merge the even indexed numbers of the two sub sequences it implies that (a₂, a₄, a₆......... a_m) and (b₂, b₄, b₆......... b_m) and so resulting in sorted sequence (d₁, d₂, d₃......... d_m).

4)  The last output sequence O= (o₁, o₂, o₃......... o_2m) is attained in the given below manner: o1 = a1 and o2m = bm .In broad the formula is as following: o2i = min (ai+1, bi) and o2I+1 = max(ai+1,bi ) for i=1,2,3,4..........m-1. 

Now let's take an illustration for merging the 2 sorted sequences of length 4 it implies that A= (a1, a2, a3, a4) and B= (b1, b2, b3, b4). Assume numbers of sequence are A= (4, 6, 9, 10) And B= (2, 7, 8, 12). The circuit of merging the two provided sequences is explained in Figure.

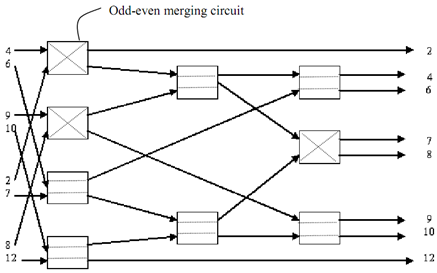
Figure: Merging Circuit