To understand the multiplication of binomials, we should know what is meant by Distributive Law of Multiplication. Suppose that we are to multiply (a + b) and m. We treat (a + b) as a compound expression and m as a simple expression.  Therefore,  (a + b)m by definition will be:

         =       m + m + m + m + ....... taken a + b times

         =       (m + m + m + .... taken a times) + (m + m + m + ..... taken b times)

         =       am + bm

Similarly (a - b)m = am - bm and (a - b + c)m = am - bm + cm. This is referred to as Distributive Law of Multiplication and it says that the product of a compound expression by a simple expression is the algebraic sum of the partial products of each term of the compound expression by that simple expression.

         In the above, if we write (c + d) in place of m we will have

         (a + b)(c + d)    =              a(c + d) + b(c + d)

                                =              ac + ad + bc + bd

1. Multiply (3a + d) and (b + c).

We employ (a + b)(c + d) = a(c + d) + b(c + d)   = ac + ad + bc + bd. Therefore, (3a + d)(b + c)   = 3a(b + c) + d(b + c) = 3ab + 3ac + bd + cd. (This procedure can be extended to trinomials and polynomials also.)

2. Multiply 2a + 5c and 3d + 2b.

         One way of doing this is to employ (a + b)(c + d) = ac + ad + bc + bd

         That is,

         (2a + 5c)(3d + 2b) = 2a(3d + 2b) + 5c(3d + 2b)

                                   = 6ad + 4ab + 15cd + 10bc

In the second method, we position the binomials as we did in addition or subtraction and do the multiplication operation. That is,

This product is the same as one obtained earlier.

Multiply

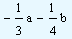and

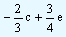That is, we have to compute

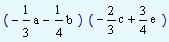
We write this as

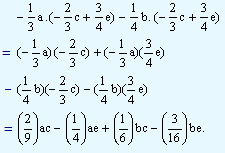
(Note: While multiplying fractions, numerators and denominators of given fractions are multiplied respectively and the product also being expressed as a fraction.)

1. Add 3ac + 5bd - 7cd and ac - 5bd - 4cd

1. Multiply 3a + 5b - 7d and c - 4e - 5

That is, we require (3a + 5b - 7d) x (c - 4e - 5)

= 3a (c - 4e - 5) + 5b (c - 4e - 5) - 7d(c - 4e - 5)

= 3ac - 12ae - 15a + 5bc - 20be - 25b - 7cd + 28de + 35d