This time we are going to take a look at an application of second order differential equations. It's now time take a look at mechanical vibrations. In exactly we are going to look at a mass which is hanging from a spring.

Vibrations can arise in pretty much all branches of engineering and thus what we're going to be doing now can be simply adapted to other situations, generally with just a change in notation.

Let's find the situation setup. We are going to begin with a spring of length l, termed as the natural length, and we're going to hook an object along with mass m up to this. While the object is attached to the spring, it will stretch a length of L. We will identify it the equilibrium position the position of the center of gravity for the object like this hangs on the spring along with no movement.

There is sketch given below, of the spring with and without the object attached to this.

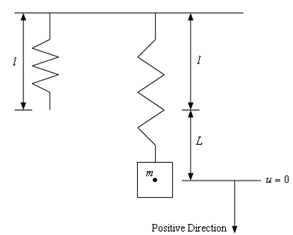
As denoted in the above sketch we are going to suppose that all velocities, forces and displacements in the downward direction will be positive. All velocities, forces and displacements in the upward direction will be negative.

Also, as demonstrated in the sketch above, we will measure all displacement of the mass by its equilibrium position. Thus, the u = 0 position will corresponding to the center of gravity for the mass as this hangs on the spring and is at rest, which is no movement.

Here, we need to develop a differential equation which will provide the displacement of the object at any time t.  Firstly, recall Newton's Second Law of Motion.

ma = F

In this case we will use the second derivative of the displacement, u, for the acceleration and so Newton's Second Law turns into,

mu′′ = F (t, u, u′)

We now require determining all the forces that will act on the object. There are four forces which we will suppose act upon the object. Two, will all the time act upon the object and two which may or may not act on the object.