Other Measures of Dispersion

In this section, we look at relatively less used measures of dispersion like fractiles, deciles, percentiles, quartiles, interquartile range and finally quartile deviation. Quartile deviation is also referred to as semi-interquartile range.

Fractiles are similar to percentages. If we say that in CFA level I, the pass percentage was 35, we understand that out of every 100 candidates who appeared for the examination, 35 candidates passed the examination. Similar to this, in a frequency distribution also there are always some elements which lie at or below the given fractile. For instance, the median is 0.50 fractile as half of the data is less than or equal to this value. Further in any distribution, 25 percent of the data lies at or below the 0.25 fractile. Interfractile range is the difference between the values of two fractiles. Therefore, this is also necessarily a measure of dispersion between the two fractiles in a frequency distribution. Depending on the number of equal parts into which we divide the data we call them as deciles, percentiles and quartiles. A decile is a fractile which divides the data into ten equal parts, percentile is a fractile which divides the data into 100 equal parts and finally a quartile is the one which divides the data into four equal parts. While computing fractiles we ought to arrange the elements in an increasing order.

Interquartile Range: Since range, interfractile and interquartile range typically from what we call as distance measures of dispersion, the interquartile range looks at how far one should go from the median on either side of it before one-half of the data points are included. As we have seen above, quartiles are fractiles which divide the data into four equal parts such that each quartile consists 25 percent of the data points. The quartiles are the highest data points in each of these four parts. Interquartile range is the difference between the last value in the third quartile (usually denoted by Q₃) and the last value in the first quartile denoted by Q₁.

Quartile Deviation: It is the difference between the third and the first quartile divided by two. It is expressed as Q.D.

Q.D.

=

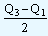where,

         Q₁ = first quartile

         Q₃ = third quartile