General Perspective transformation with COP at the origin

Here we suppose the given point P(x,y,z) be projected like P'(x',y',z') on the plane of projection. The center of projection is at the origin, determined by O(0,0,0). Let the plane of projection explained by the normal vector N=n₁I+n₂J+n₃K and passing via the reference point R₀(x₀,y₀,z₀). By Figure 21, the vectors PO and P'O have the similar direction. The vector P'O is a factor of PO. Thus they are associated through the equation of: P'O = α PO, comparing elements we have x'=α.x   y'=α.y   z'=α.z we here get the value of α.

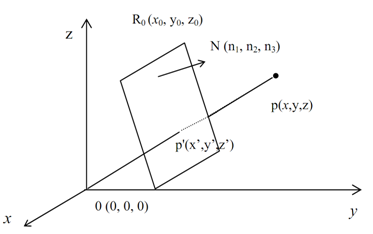
We know about the equation of the projection plane passing via a reference point R₀ and having a common vector as N=n₁I+n₂J+n₃K is specified by PR₀.N=0, which is:

(x-x₀,y-y₀,z-z₀).( n₁,n₂,n₃)=0 which is n₁.( x-x₀)+ n₂.( y-y₀)+ n₃.( z-z₀)=0 ---------( )

Because P'(x',y',z') lies upon this plane, hence we have as:

n₁.( x'-x₀)+ n₂.( y'-y₀)+ n₃.( z'-z₀)=0

Once substituting x'=α.x ;  y'=α.y ;  z'=α.z, we have as:

α =(n₁.x₀+ n₂.y₀+ n₃.z₀)/(n₁.x+ n₂.y+ n₃.z) = d₀/(n₁.x+ n₂.y+ n₃.z)

This projection transformation cannot be shown as a 3x3 matrix transformation. Conversely, by utilizing the HC representation for 3-D, it can write in projection transformation as:

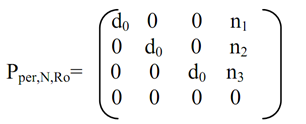
Hence, the projected point P'h(x',y',z',1) of given point Ph(x, y, z, 1) can be acquired as:

P'_h = P_h. P_per,N_, R_o = [x, y, z, 1]  

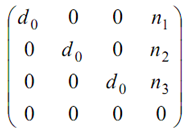
= [d₀.x, d₀.y, d₀z, (n₁.x + n₂.y + n₃.z)] ;

Here d₀ = n₁.x₀ + n₂.y₀ + n₃. z₀.