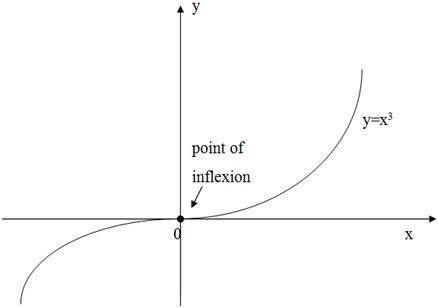
Example of inflection point

Determine the points of inflection on the curve of the function

y = x³

Solution

The only possible inflexion points will happen where

(d²y)/( dx²)   = 0

From specified function as:

(dy)/(dx) = 3x² and (d²y)/( dx²)   = 6x

Equating the second derivative to zero, we include

 6x = 0 or x = 0

We test whether the point at that x = 0 is an inflexion point as follows

While x is slightly less than 0, ((d²y)/(dx²)) < 0; it means a downward concavity

While x is slightly larger than 0, ((d²y)/(dx²)) > 0;  it means an upward concavity

Hence we have a point of inflexion at point x = 0 since the concavity of the curve changes as we pass from the left to the right of x = 0

Illustration:-

maximize and the revenue

1. The per week revenue Sh. R of a small company is specified by

 R = (14 + 81x - (x³/12)) whereas x is the number of units produced.

Required

i.          Find out the number of units that maximize the revenue

ii.         Find out the maximum revenue

iii.        Find out the price per unit that will maximize revenue

Solution

i. To determine maximum or minimum value we needs differential calculus as given below:

R = (14 + 81x - (x³/12))

(dR)/(dx) = 81 - (1/12) . (3x²)

(d²R)/(dx²) = 0 - (1/12) . (3.2x) = -(x/2)

Put (dR)/(dx) = 0 that is 81 - (1/4)x² = 0

That gives x = 18 or x = -18

(d²R)/(dx²) = -(x/2)

Hence when x = 18;

(d²R)/(dx²) = -9

That is (-) negative indicating a maximum value.

Hence at x = 18, the value of R is a maximum. Correspondingly at x = -18, the value of R is a minimum. Thus, the number of units that maximize the revenue = 18 units

i. The maximum revenue is given as

            R = 14 + 81 + 18 - ((18)³)/12

                        = Shs. 986

ii.The price per unit to maximize the revenue is given as:

986/18 = 54.78 or Shs.54.78