Evaluate following limits.
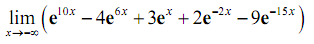
Solution: Let's begin this one off in the similar manner as the first part. Let's take the limit of each piece. This time note that since our limit is going to negative infinity the first three exponentials will actually go to zero (since their exponents go to minus infinity in the limit). The final two exponentials will go towards infinity in the limit (since their exponents go to plus infinity in the limit).
Taking limits gives,
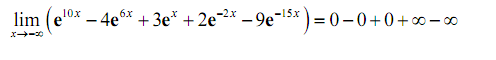
Thus, the last two terms are the problem as they once again leave us with an indeterminate form. We will factor out the "largest" exponent in the last two terms. However "largest" doesn't refer to the bigger of the two numbers (-2 is bigger than -15). Rather than we're going to utilize "largest" to refer to the exponent i.e. farther away from zero. By using this definition of "largest" means that we're going to factor out an e-15 x.
Again, remember that to factor out this all we actually are doing is dividing each of the term by e-15 x and then subtracting exponents. Following is the work for the first term as an example,
e10 x /e-15 x = e10 x-( -15 x)= e25 x
As along the first part we can either factor out it of only the "problem" terms (that means the last two terms), or all the terms. For the practice we'll factor it out of all the terms. Following is the factoring work for this limit,
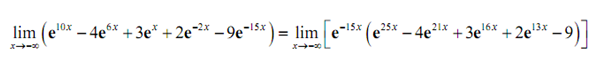
At last, after taking the limit of the two terms (the first is infinity & the second is a negative, finite number) and recalling the Facts through the Infinite Limit section we see that the limit is,
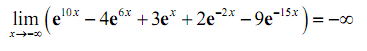
At last, as you might have been capable to guess from the previous example while dealing with a sum and/or difference of exponentials all we have to do is look at the largest exponent to find out the behavior of the whole expression. Again, recalling that if the limit is at plus infinity we just see at exponentials along with positive exponents & if we're looking at a limit at minus infinity we just see at exponentials with negative exponents.