Q - Derive bending equation that is,; M/I =  σ /y = E/R.                                                                          

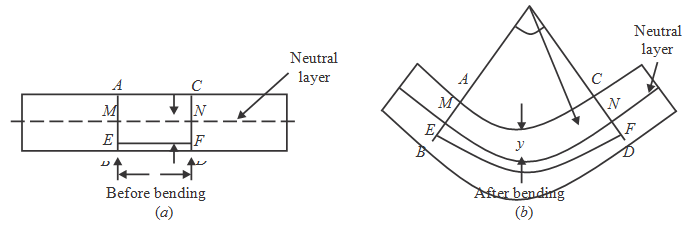
Sol.: With reference to the figure given to us, consider any two normal sections AB and CD of a beam at small distance   δ L apart (that is, AC = BD = δ L). Let AB and CD intersect neutral layer at the points M and N respectively.

Let;

M = bending moment acting on beam

θ = Angle subtended at centre by the arc.

R = Radius of curvature of neutral layer M' N' .

At any distance 'y' from neutral layer MN, consider layer EF.

As shown in the figure the beam because of sagging bending moment. After bending, A' B', C' D' , M' N'  and

E'F' represent final positions of AB, CD, MN and EF in that order.

When produced, A' B' and C' D' intersect each other at the O subtending an angle θ radian at point O, which is centre of curvature.

As   L is quite small, arcs A' C' , M' N' , E' F'  and B' D'  can be taken as circular.

Now, strain in layer EF because of bending can be given by e = (E F  - EF)/EF = (E F  - MN)/MN

As MN is the neutral layer, MN = M' N'

 
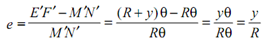
Let; σ  = stress set up in layer EF  because of bending

E = Young's modulus of material of beam.

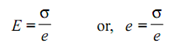
Equate the equation (i) and (ii);
  

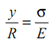
Let;       σ = stress set up in layer EF because of bending

E = Young's modulus of material of beam.

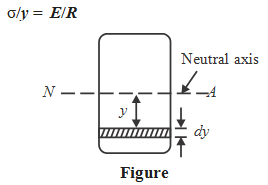
At distance 'y', let us consider an elementary strip of quite small thickness dy. We have already assumed that 'σ ' is bending stress in this strip.

Let dA = area of the elementary strip. Then, force developed in this strip =   σ.dA.

Then the, elementary moment of resistance because of this elementary force can be
given by dM = f.dA.y

Total moment of resistance because of all such elementary forces can be given by

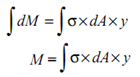
From the Equation (iii),

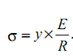
By putting this value of  f in Equation (iv), we get

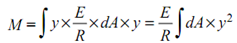
But

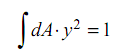
where  I = Moment of inertia of whole area about neutral axis N-A.

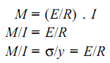
Where;

M = Bending moment

I  = Moment of Inertia about axis of bending that is; Ixx

y  = Distance of the layer at which the bending stress is consider

(We take always the maximum value of y, that is, distance of extreme fiber from N.A.)

E = Modulus of elasticity of beam material.

R = Radius of curvature