This question is designed to give you practice in manipulating circuit equations using j notation, and to demonstrate that techniques that you have already studied in the d.c. context can be applied equally successfully to the solution of steady-state a.c. problems.
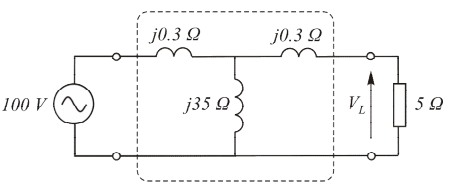
The sketch (right) shows the approximate equivalent circuit of a real transformer (inside the dotted line) with its parameters referred to the primary side, and with a referred load resistance of 5 ω. Find
(a) the open-circuit voltage VL , and
(b) the voltage across the 5 ω 'referred' load, by the following three methods.
Method 1: Direct approach. First find the open circuit voltage by simple 'potential divider' approach (but with complex impedances Z replacing the simple resistances we used under d.c. conditions). Then find the equivalent series impedance of the two parallel branches on the right, and again use the 'potential divider' idea to find VL. The calculations are lengthy, and you will probably find it best to use polar form for the multiplications and divisions.
Method 2: Thévenin. Find the Thévenin equivalent circuit for the transformer and 100 V supply. Then apply the load and use the potential divider approach.
Method 3: Nodal Analysis. Call the node at the top of j35 node a and that at the top of the 5 ω load node b, with the reference (zero) node at the bottom. Write down the nodal equations in terms of the complex impedances, and solve for Vb.
Calculate the % change in the output voltage when the load is applied (this is known, as the 'regulation'). What would you expect the regulation to be if the transformer were ideal?