Q. Describe what do you understand by the term array? How does an array vary from an ordinary variable? How are the arrays represented in the specific memory?
Ans.
Array Vs. Ordinary Variable is explained as follows
Array is made from the similar data structure that exists in any language. Array is the set of similar or alike data types. Array is the collection of similar or alike elements. These similar or alike elements could be all int or all float or all char etc. Array of char is called as string. All elements of the given array should be of same type. An array is finite ordered set of the homogeneous elements. The number of elements in the array is pre- determined.
For example. Ordinary variable: - int a
Array: - int a[10]
An ordinary variable of a simple data type can save a single element only
Representation of Array in memory is shown below
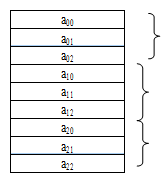
Assume a be a 2 dimensional m x n array
|
|
Col 0
|
Col 1
|
Col 2
|
|
Row 0
|
a00
|
a01
|
a02
|
|
Row 1
|
a10
|
a11
|
a12
|
|
Row 2
|
a20
|
a21
|
a22
|
Though a is pictured as a rectangular pattern with in row and n column it is represented in memory or a particular location by a row of m x n elements. Sequential memory locations the element can be saved in row major order.
Column major order is explained as follows:- the elements are saved column by column i.e. m elements of the 1st column is saved in first m locations, elements of the 2nd column are saved in next m location and so on..
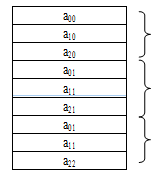
Row major order is shown below:-
The elements are saved row by row ie. N elements of the 1st row are saved in 1st n location, elements of 2nd row are saved in next n location, and so on