Approximating solutions to equations : In this section we will look at a method for approximating solutions to equations. We all know that equations have to be solved on occasion and actually we've solved out quite a few equations by ourselves to this point. In all the instances we've looked at to this instance we were capable to in fact find the solutions, however it's not always probable to do that exactly and/or do the work by hand.
That is where this application comes into play. Therefore, let's see what this application is all about.
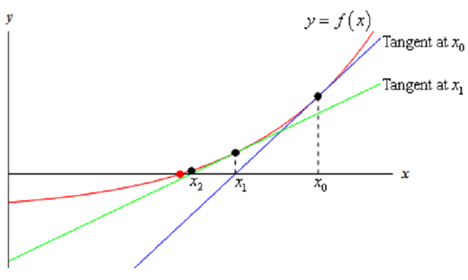
Let's assume that we desire to approximate the solution to f (x) = 0 and let's also assume that we have somehow found an initial approximation to this solution say, x0. This initial approximation is perhaps not all that good and therefore we'd like to discover a better approximation. It is easy enough to do. Firstly we will get the tangent line to f ( x )at x0.
y = f ( x0 ) + f ′ ( x0 ) ( x - x0 )
Now, take a look at the graph below.
The blue line (if you're reading this in color anyway...) is the tangent line at x0. We can illustrate that this line will cross the x-axis much closer to the actual solution to the equation than x0 does. Let's call this point where the tangent at x0 crosses the x-axis x1 and we'll utilizes this point as our new approximation to the solution.
Therefore, how do we determine this point? Well we know it's coordinates, ( x1 ,0) , and we know that it's on the tangent line therefore plug this point into the tangent line & solve out for x1 as follows,
0 = f ( x0 ) + f ′ ( x0 ) ( x1 - x0 )
x - x0 = - f (x0 ) /f ′ ( x0 )
x1 = x0 - (f ( x0 ) /f ′ ( x0 ))
Therefore, we can determine the new approximation provided the derivative isn't zero at the original approximation.
Now we repeat the whole procedure to determine an even better approximation. We build up the tangent line to f ( x ) at x1 and utilizes its root, that we'll call x2, as a new approximation to the actual solution. If we do it we will arrive at the given formula.
x2= x1 - (f ( x1 ) /f ′ ( x1 ))
This point is also illustrated on the graph above and we can illustrated from this graph that if we continue following this procedure will get a sequence of numbers which are getting very close the real solution. This procedure is called Newton's Method.