The 3-D Coordinate System
We will start the chapter off with a quite brief discussion introducing the 3-D coordinate system and the conventions that we will be utilizing. We will as well take a concise look at how the different coordinate systems can alter the graph of an equation.
Let us first get some basic notation out of the way. The 3-D coordinate system is frequently denoted by R3. Similarly the 2-D coordinate system is frequently denoted by R2 and the 1-D coordinate system is represented by Rn. As well, as you might have guessed then a general n dimensional coordinate system is frequently denoted by Rn.
Subsequently, let's take a quick look at the basic coordinate system.
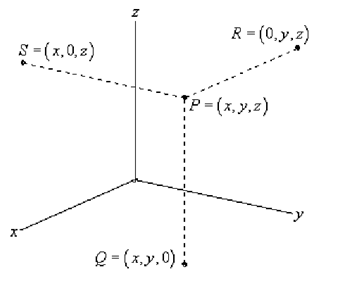
The above is the standard placement of the axes in this class. It is supposed that only the positive directions are displayed by the axes. If we require the negative axes for any reason we will put them in as required.
As well note the various points on this sketch. The point P is the common point sitting out in 3-D space. If we begin at P and drop straight down until we arrive a z-coordinate of zero we arrive at the point Q. We state that Q sits in the xy-plane. The xy-plane refers to all the points that have a zero z-coordinate. We can as well start at P and move in the other two directions as displayed to get points in the xz-plane (this is S along with a y-coordinate of zero) and the yz-plane (this is R along with an x-coordinate of zero).
Jointly, the xy, xz, and yz-planes are occasionally termed as the coordinate planes.
As well, the point Q is often considered to as the projection of P in the xy-plane. Similarly, R is the projection of P in the yz-plane and S is the projection of P in the xz-plane.
Several formulas that you are employed to working with in R2 have natural extensions in R3.