Reference no: EM131207950

1. The Simple Linear Model

The simple linear regression tries to better understand the functional dependence of one variable on another. In particular, consider a relationship of the form

Y_i = α + β + ε_i

where Y_i is a random variable and xi is another observable variable. The quantities α and β, the intercept and slope of the regression, are assumed to be fixed and unknown parameters, and ε_i is another random variable. It is also common to suppose that E[ε_i] = 0 (otherwise we could just rescale the excess into α), so that we have

E[Y_i|x_i] = α + βx_i

This relationship is called the population regression function. One main purpose of regression is to predict Y_i from knowledge of x_i. We can also define the following sum of squares:

S_xx = _i=1∑ⁿ (x_i - x^-)²

S_yy = _i=1∑ⁿ(y_i - y^-)²

S_xy = _i=1∑ⁿ(x_i - x^-)(y_i - y^-)

RSS(a, b) = _i=1∑ⁿ (y_i - a - bx_i)²

[1] Use the least squares approach to show that the estimators for α and β are:

α^{^} = y^- - β^{^}x^-

β^{^} =  S_xy/S_xx

[2] Let y^{^}_i = α^{^} + β^{^}x_i and u^{^}_i = y_i - y^{^}_i. Show that:

_i=1∑ⁿ u^{^}_i = 0

_i=1∑ⁿu^{^}_ix^{^}_i = 0

The conditional normal model is the one of the most common simple linear regression models. The observed data are pairs, (x₁, Y₁), . . .  ,(x_n, Y_n). The values of the predictor variable, x₁, . . . ,x_n are considered to be known, fixed constants (you can think of them as being chosen and set by the experimenter). The random variables Y₁, . . . , Y_n are assumed to be independent. Furthermore,

Y_i = α + βx_i + ε_i

where ε₁, . . . ,ε_n are i.i.d. N(0, σ²), which implies that the distribution of Y_i is also normal:

Yi _~ N(α + βx_i, σ²)

Thus, the population regression function is a linear function of x, that is, E(Y|x) = α + βx.

[3] Write down the likelihood function for the model, that is, the joint pdf of Y₁, . . . ,Y_n.

[4] Show that, for fixed values of σ², maximizing the log likelihood function is equivalent of minimizing:

_i=1∑ⁿ(Y_i - α - βx_i)²

And then the estimators are the same as in [2].

[5] Show that:

[Hint: find the expected value, variance and covariance of the estimators, and finally argue that they are normally distributed.]

[6] An unbiased estimator for σ² is:

S² = (1/n-2)_i=1∑ⁿ(Y_i - α^{^} - β^{^}x_i)²

Use the fact that S² is independent of (α^{^}, β^{^}) and the following distributional result:

(n -2)S²/σ² _~ χ²_n-2

to find a 100(1 - α)% confidence interval for β. Also explain how you would test H₀: β = β₀ vs H₁: β ≠ β₀.

Now you will study prediction analysis. Assume that (x₁, Y₁), . . . ,(x_n, Y_n) satisfy the conditional normal regression model, and based on these n observations we have the estimates, α^{^}, β^{^} and S². Let x₀ be a specified value of the predictor variable. First, consider estimating the mean of the Y population associated with x₀, that is, E(Y|x₀) = α + βx₀. The obvious choice for a point estimator is α^{^} + β^{^}x₀.

[7] Show that:

α^{^} + β^{^}x_{0 ~} N(α + βx₀, σ²(1/n + ((x₀ - x^-)²/S_xx)))

[Hint: find the expected value and variance of the estimator, and finally argue that it is normally distributed.]

[8] Use that

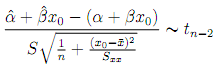
To find a 100(1- α)% confidence interval for the prediction.

Now you will asses the performance of the estimators in a simulation study using R. For all the questions below, use the following setup for i = 1, . . . ,n:

ε_{i ~} N(0, 1)

x_{i ~} U(0, 2)

Y_i = α + βx_i + ε_i

α = β = 1
Also use set.seed(520) for easy comparison of the results.

[9] Generate 1,000 random samples of size n = 500 and, for each simulation, compute α^{^}, β^{^} and S². Plot the three densities and discuss the results.

[10] Let x₀ = 1. Using the previous simulation study, compute also the distribution of the estimator for the predicted value α^{^} + β^{^}x₀. That is, for each simulation run, compute the point estimator and its variance from problem [7]. Finally, also compute the confidence interval from [8] and check if it has the right coverage.

2. The Generalized Linear Model

A generalized linear model (GLM) describes a relationship between the mean of a response variable Y and an independent variable x. But the relationship may be more complicated than the E[Y_i] = α + βx_i of the simple linear model from Section I. Many different models can be expressed as GLMs.

A GLM consists of three components: the random component, the systematic component, and the link function.

1. The response variables Y₁, . . . ,Y_n are the random component. They are assumed to be independent random variables, each with a distribution from a specified exponential family. The Y_is are not identically distributed, but they each have a distribution from the same family: binomial, Poisson, normal, etc.

2. The systematic component is the model. It is the function of the predictor variable X_i, linear in the parameters, that is related to the mean of Y_i. We will consider only α + βx_i here.

3. Finally, the link function g(μ) links the two components by asserting that g(μ_i) = α + βx_i, where μ_i = [Y_i].

In probit regression, the link function is the standard normal cdf Φ (x) = P(Z ≤ x), where Z _~ N (0, 1). Thus, in this model we observe (Y₁, x₁), (Y₂, x₂), . . . ,(Y_n, x_n), where Y_{i ~} Bernoulli(π_i) and π_i = P(Y_i = 1) = Φ(α + βx_i).

[1] Derive the pdf Y_i and compute E[Y_i] and Var [Y_i].

[2] Find the likelihood function of Y₁, . . . ,Y_n.

[3] Using the log-likelihood function, show that the first order condition for α and β are:

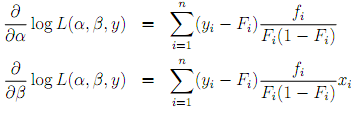
and find the exact expressions for F_i and f_i.